GAS HYDRATE STRUCTURE 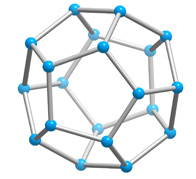
With a few important exceptions, the structural feature common to all clathrate hydrates is the pentagonal dodecahedron 512 (D) of water molecules. It has 12 regular pentagonal faces, 20 vertices, and 30 edges.
As an H40O20 unit of water structure, each vertex is the site of an oxygen atom and each edge an 0—H .... 0 hydrogen bond. Hence, of the 40 protons, 30 are located in the edges. If a fourth external hydrogen bond is formed to another water molecule at each oxygen atom, the distribution of the protons can be such that each oxygen atom in the polyhedron is half donor and half acceptor relative to its four nearest neighbors.
Moreover, the oxygen coordination is very close to tetrahedral, with three angles at 108° and three at 110.9°. A first-neighbor environment of each water molecule is therefore, very similar to that in hexagonal or cubic ice. 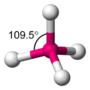
Unlike the tetrahedron and cubooctahedron, the dodecahedron is not a space-filling solid, nor are its fivefold symmetry axes compatible with a homogenous space-filling arrangement with long-range periodicity. With small distortions, it occurs in clathrate crystal structures with other polyhedra so that together they satisfy the requirements for a periodic lattice. These polyhedra are 51262 (T, 14-hedron, consisting of twelve pentagonal and two hexagonal faces), 51263 (P,15-hedron, consisting of twelve pentagonal and three hexagonal faces ,and 51264 (H, 16-hedron, consisting of twelve pentagonal and four hexagonal faces).
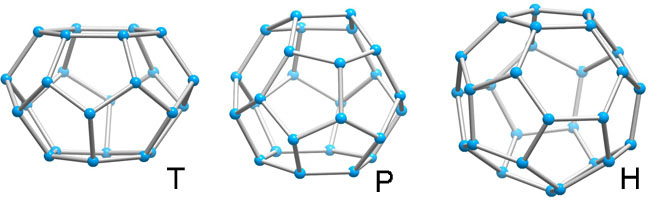
Above polyhedra are deceptively simple in appearance. They can almost, but not quite, be closed by regular pentagonal and hexagonal plane faces. For example, the nearest approach to regularity for the T cage has a ratio of edge length of hexagon to pentagon of 1.15 and angles in the pentagons of 110°18', 101°54', 115°36', 101°54', 110°18'.
Clathrates are potentially nonstoichiometric compounds, since all the voids need not necessarily be occupied in order to form a stable crystalline material. Barrer and Stuart and van der Waals and Platteeuw, in their statistical thermodynamic treatments of the gas hydrate system, applied the cell theory of liquids to a model in which the clathrate is regarded as a solution of the gaseous guest in the solid host with fractional occupancy factors of the voids. These calculations gave good agreement with the observed dissociation pressures for small symmetrical molecules but were less successful for the diatomic and larger guests, where there may be some hindrance to free rotation within the voids.
With an oxygen nonbonding radius of 1.4 A, the free diameter within a pentagonal dodecahedron (D) is 5.0 A; the 14-hedra (T)and 15-hedra (P) are approximately oblate and prolate spheroids with diameters 5.3 and 6.4 A, 6.1 and 7.0 A, respectively; the 16-hedra (H) is nearly spherical with diameter 6.6 A. It might be anticipated, therefore, that the cohesive forces across these polyhedra would be such as require that at least the majority of the larger voids be occupied in order to form the clathrate water structure rather than ice at the freezing point. It is noteworthy that the most stable hydrates are those for which the vacant lattice has the greatest density.
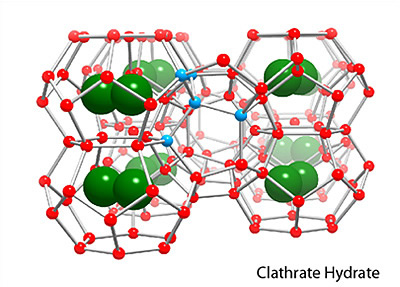
Two main gas hydrate structures are cubic type I and type II. Type I unit cell is 12 A and consists of 2D cages and 6T cages (46 water molecules). Type II unit cell is 17 A and consists of 16D and 8H cages (136 water molecules).
Photos of two main gas hydrate structures constructed in Janda Lab from plastic kits:
TYPE I CLATHRATE HYDRATE TYPE II CLATHRATE HYDRATE
* Udapted from Jeffrey and McMullan, The Clathrate Hydrates, 1967








