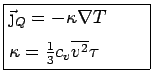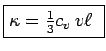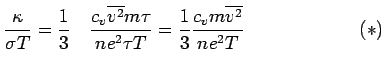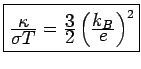Next: Seebeck Effect - Thermopower
Previous: lecture2
Drude Theory of Thermal Conductivity
The thermal conductivity 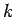 is defined as the proportionality
constant in Fourier's law:
is defined as the proportionality
constant in Fourier's law:
where
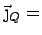 heat current = heat transported across a unit area
per unit time.
heat current = heat transported across a unit area
per unit time.
In Drude's model, electrons transport heat because the electrons
thermalized at the ``local" temperature of the last collision.
(Assume thermalization at each collision.) Thus, the electrons
leaving the hotter regions carry more energy. Let's derive Fourier's
law and derive an expression for 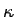 . We will use the same
approach that we used for deriving
. We will use the same
approach that we used for deriving 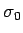 . Look at
. Look at
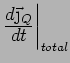 . There are 2 contributions -
diffusion and collisions (which knock electrons out of the right
direction):
. There are 2 contributions -
diffusion and collisions (which knock electrons out of the right
direction):
What is
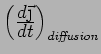 ?
Suppose the system has a temperature gradient but no collisions (save
those for the other term). Consider the electrons which cross the
plane
?
Suppose the system has a temperature gradient but no collisions (save
those for the other term). Consider the electrons which cross the
plane 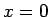 at a time
at a time 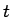 after the start of the operation. An
electron with velocity
after the start of the operation. An
electron with velocity 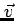 will have come from a point
will have come from a point
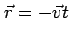 away and will therefore have the average energy appropriate
for that point, i.e.,
away and will therefore have the average energy appropriate
for that point, i.e.,
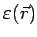 . The extra energy will be
. The extra energy will be
The ``extra" energy current is
Since the velocity distribution is approximately isotropic (nothing
makes the electrons go in the 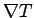 direction), the energy
diffusion is along
direction), the energy
diffusion is along 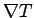 .
.
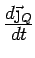 has a component only along
has a component only along 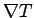 and we can replace the
and we can replace the 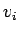 's with
's with
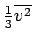 . This gives
. This gives
where the energy per unit volume
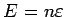 , and
, and
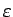 is the energy
per particle.
is the energy
per particle.
Collisions Now put in collisions. We assume that the
electrons thermalize at every collision. Thus the extra heat current
carried by an electron is annihilated at every collision.
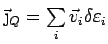 is also lost and we can simply write
is also lost and we can simply write
Thus
In steady state,
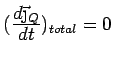 .
Using
.
Using
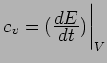 gives the standard Kinetic
Theory of Gases result:
gives the standard Kinetic
Theory of Gases result:
To the extent that
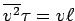 ,
,
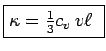
Wiedemann-Franz Law
It is an empirical fact that
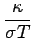 |
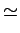 |
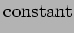 that is nearly the same
in all metals that is nearly the same
in all metals |
|
| |
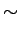 |
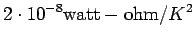 |
|
(See Table 1.6 in AM).
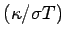 is called the Lorenz number. Can the Drude theory explain this? We have
is called the Lorenz number. Can the Drude theory explain this? We have
Thus
Now if one uses a simple Kinetic Theory of Gases picture for a monatomic gas:
This is
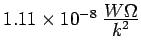 , i.e.,
almost exactly half the experimental value. We will see later that Eq.
(
, i.e.,
almost exactly half the experimental value. We will see later that Eq.
( ) is in fact approximately right: it is the evaluation of
) is in fact approximately right: it is the evaluation of 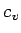 and
and
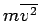 that is wrong. Fortuitously, the mistakes cancel
except for a factor of 2. Incidentally, there was no evidence in
Drude's time for an electronic specific heat of
that is wrong. Fortuitously, the mistakes cancel
except for a factor of 2. Incidentally, there was no evidence in
Drude's time for an electronic specific heat of
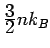 .
.
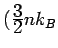 is a lot of specific heat.)
So it was puzzling as to why the Lorenz number came out
correctly when it appeared that there was no
is a lot of specific heat.)
So it was puzzling as to why the Lorenz number came out
correctly when it appeared that there was no 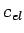 at room
temperature.
at room
temperature.
Subsections



Next: Seebeck Effect - Thermopower
Previous: lecture2
Clare Yu
2006-10-03
![]() is defined as the proportionality
constant in Fourier's law:
is defined as the proportionality
constant in Fourier's law:
![]() . We will use the same
approach that we used for deriving
. We will use the same
approach that we used for deriving ![]() . Look at
. Look at
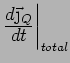 . There are 2 contributions -
diffusion and collisions (which knock electrons out of the right
direction):
. There are 2 contributions -
diffusion and collisions (which knock electrons out of the right
direction):

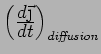 ?
Suppose the system has a temperature gradient but no collisions (save
those for the other term). Consider the electrons which cross the
plane
?
Suppose the system has a temperature gradient but no collisions (save
those for the other term). Consider the electrons which cross the
plane 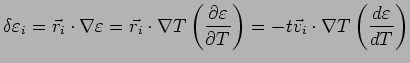
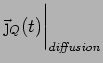
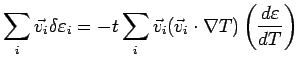
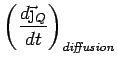
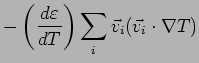
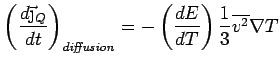
![]() is also lost and we can simply write
is also lost and we can simply write
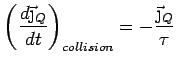
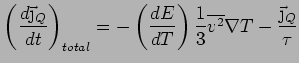
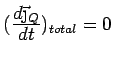 .
Using
.
Using
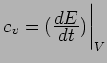 gives the standard Kinetic
Theory of Gases result:
gives the standard Kinetic
Theory of Gases result: