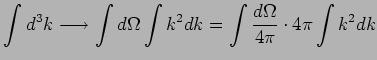 |
Most of the properties of the electron states are governed by energy,
and sometimes, direction of propagation. So it is convenient to write
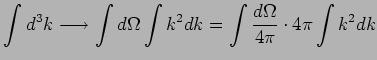 |
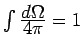 and we are left with
and we are left with
Often it is more convenient to integrate over energy. Since
![]() depends only on the magnitude of
depends only on the magnitude of ![]() ,
,
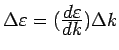 .
.
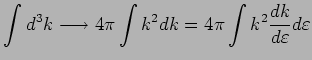 |
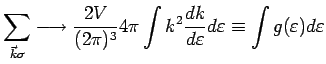 |
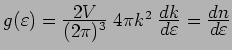 is the number of states in the
interval
is the number of states in the
interval
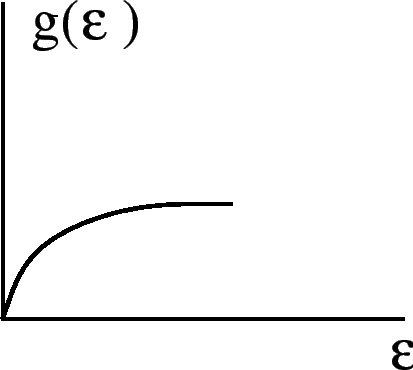
For a free electron gas,
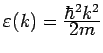 ,
,
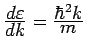
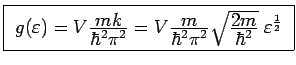
Fermi-Dirac Statistics
Electrons are fermions, hence the total wavefunction is
antisymmetric. There can be no more than one electron per state
![]() . At
. At ![]() , the ground state is obtained by filling
up the lowest possible energy states (assuming a fixed number of
electrons). In this way, we fill up a sphere in
, the ground state is obtained by filling
up the lowest possible energy states (assuming a fixed number of
electrons). In this way, we fill up a sphere in ![]() -space. The
radius of the sphere is fixed by the condition
-space. The
radius of the sphere is fixed by the condition
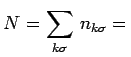 total number of
occupied states total number of
occupied states |
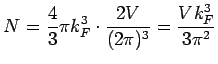 |
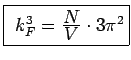
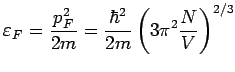 |
Typical values:
![]() cm
cm![]() (
(
![]() ),
),
![]() cm/sec
cm/sec ![]() c),
c),
![]() a few eV
a few eV ![]() atomic
energies which is no coincidence. We can also define a Fermi temperature
atomic
energies which is no coincidence. We can also define a Fermi temperature
![]() .
.
![]() . (Note
. (Note ![]() for all temperatures where substance is a solid or a liquid.)
for all temperatures where substance is a solid or a liquid.)