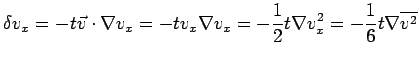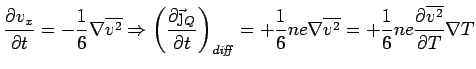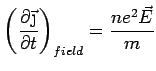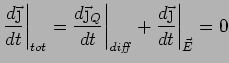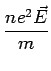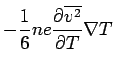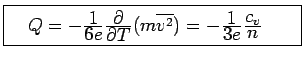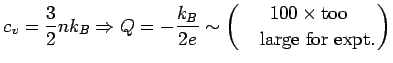Next: Quantum Theory of Electrons
Up: Lecture 2
Previous: Lecture 2
=2.5 true in
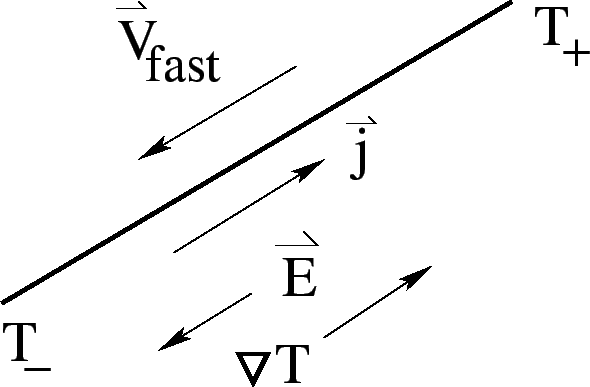
The fact that higher energy electrons move faster means that setting
up a temperature gradient would give rise to an electric current.
So, if we could set up a temperature gradient on a closed circuit, a
current would flow up the gradient (since electrons are
negatively charged). On an open circuit, the flow gives rise to a
build-up of charge at the ends, and a steady state is obtained when
the field 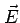 produced is sufficient to cancel the drift. Hence we
expect
produced is sufficient to cancel the drift. Hence we
expect
where the thermopower 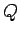 should be
should be 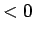 .
.
Let's calculate 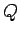 in the Drude model.
in the Drude model.
Strategy: In steady state
Diffusion
=2.5 true in
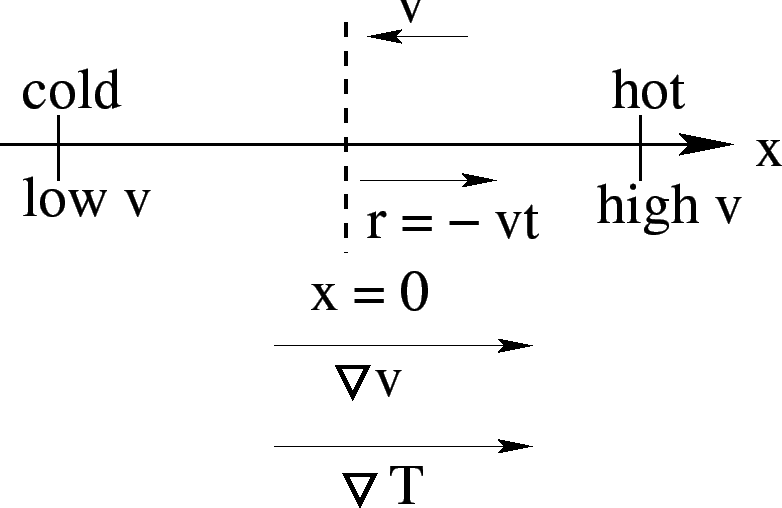
Suppose the gradient is along the 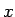 -direction. Consider the
electrons crossing the
-direction. Consider the
electrons crossing the 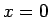 plane a time
plane a time 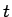 after the start of
the operation. An electron with velocity
after the start of
the operation. An electron with velocity 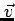 will come from a
point
will come from a
point
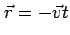 away and will have a velocity appropriate to
away and will have a velocity appropriate to
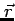 . Let
. Let
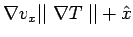 .
The excess velocity at
.
The excess velocity at 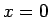 for the
for the 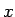 -component is
-component is
where we used
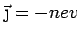 .
.
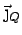 is the electric current due
to the thermal gradient.
is the electric current due
to the thermal gradient.
E-field current
Recall
Steady-State: (Heat current cancels 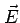 -field current)
-field current)
where
In the Kinetic Theory of Gases,



Next: Quantum Theory of Electrons
Up: Lecture 2
Previous: Lecture 2
Clare Yu
2006-10-03


![]() produced is sufficient to cancel the drift. Hence we
expect
produced is sufficient to cancel the drift. Hence we
expect
![]() in the Drude model.
in the Drude model.

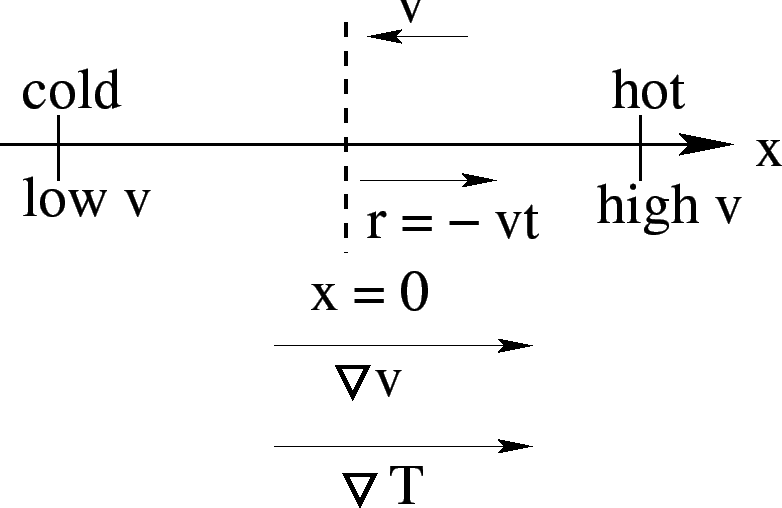
![]() -direction. Consider the
electrons crossing the
-direction. Consider the
electrons crossing the ![]() plane a time
plane a time ![]() after the start of
the operation. An electron with velocity
after the start of
the operation. An electron with velocity ![]() will come from a
point
will come from a
point
![]() away and will have a velocity appropriate to
away and will have a velocity appropriate to
![]() . Let
. Let
![]() .
The excess velocity at
.
The excess velocity at ![]() for the
for the ![]() -component is
-component is