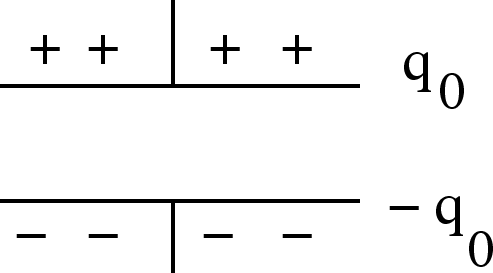Next: About this document ...
Key Points on Chapter 21: Current and Direct
Current Circuits
- is the amount of charge passing by per unit time.
- The unit of electric current is the .
- The rule states that the total current flowing into
a junction must equal the total current flowing out of the junction.
- The is the current per unit cross-sectional
area of the conductor.
- is due to electrons hitting things.
- The ratio of voltage over current is .
- The unit of resistance is the .
- Ohm's law is .
- is the inverse of resistivity.
- depends on the material, not on its size or geometry.
- Resistance is proportional to times length, and
inversely proportional to area.
- Resistance leads to .
- The amount of work done per unit charge is called the .
- In the rule, sum the changes in potential
in going around a loop of the circuit.
- resistances in series to find the equivalent
resistance.
- To find the equivalent resistance for resistors in parallel, sum the resistances.
- In an RC circuit with a capacitor and resistor in series, the characteristic
time to charge or discharge the capacitor is .
Lectures on Chapter 21: Current and Direct
Current Circuits
Current
is the amount of charge passing by per unit time.
An electric current is a stream of moving charge, e.g., a stream of conduction
electrons moving through a copper wire. Note that the wire is electrically
neutral since the copper atoms (or ions) are a fixed background through which
the electrons move.
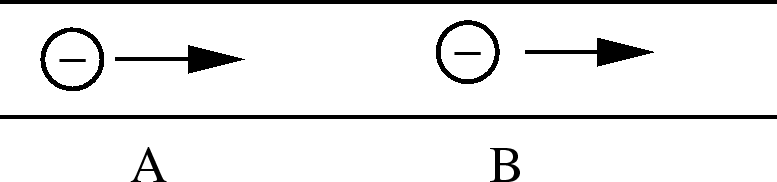
Analogy: water in a hose. Water in a hose is not an electric
current since the moving water molecules are neutral. Another
analogy is car flow down the freeway. Charge is conserved; an
electron entering one end of the wire comes out the other; it doesn't vanish in
the middle somewhere. Same for water in a hose - water that goes into the hose
comes out of the hose. The current flowing past A must also flow past B.
=2.0 true in
=2.0 true in
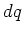 is the amount of charge passing through the plane in
a time
is the amount of charge passing through the plane in
a time 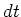 , then the current
, then the current 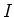 is given by
is given by
The current is the amount of charge passing through the plane per unit time.
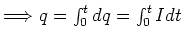 is the amount of
charge passing through the plane in the time interval from
is the amount of
charge passing through the plane in the time interval from 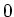 to
to 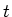 .
.
=2.0 true in
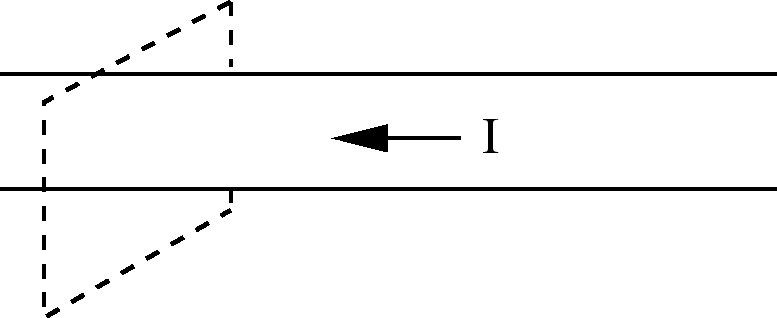
The unit of electric current is the .
Units:
![$[I] = {\rm Coulombs}/{\rm sec} = {\rm amperes}$](img14.png) (amperes = "amp").
(amperes = "amp").
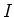 is a scalar (a number), not a vector. But an arrow is used to show the
direction of current flow. The arrow is in the direction that
positive carriers
would flow.
is a scalar (a number), not a vector. But an arrow is used to show the
direction of current flow. The arrow is in the direction that
positive carriers
would flow.
The rule states that the total current flowing into
a junction must equal the total current flowing out of the junction.
If the circuit branches,
=2.0 true in
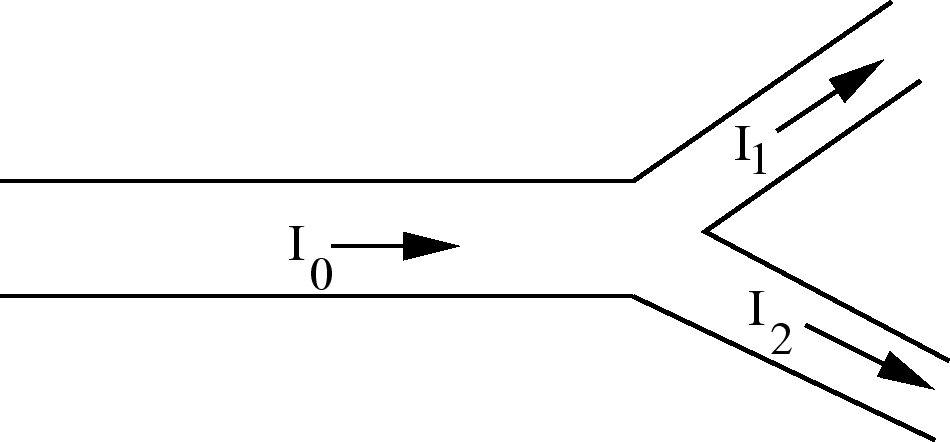
because charge is conserved. This is called the junction rule.
It is one of Kirchhoff's rules. It is important in analyzing circuits.
Current Density
The is the current per unit cross-sectional
area of the conductor.
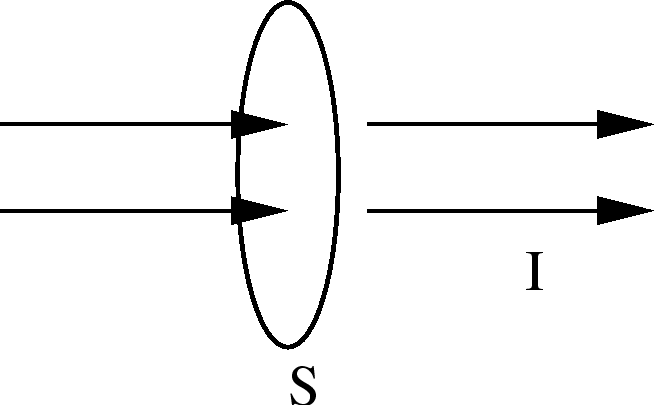
For a current that is uniform over the cross section of a wire,
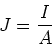 |
(1) |
where 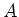 is the cross sectional area of the conductor or wire.
Cross-sectional area: Think of slicing salami. The area of
the salami slice is the cross sectional area.
The current density
is the cross sectional area of the conductor or wire.
Cross-sectional area: Think of slicing salami. The area of
the salami slice is the cross sectional area.
The current density 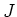 is the current per unit cross-sectional area of the
conductor.
is the current per unit cross-sectional area of the
conductor.
Units: [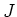 ] = Ampere/m
] = Ampere/m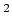
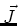 is a vector that points in the direction of
is a vector that points in the direction of 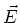 . (We need
. (We need
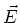 to make current flow.) The total current
to make current flow.) The total current 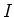 through a
surface
through a
surface 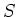 is
is
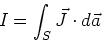 |
(2) |
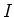 is the flux of the current density
is the flux of the current density 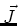 through a surface
through a surface 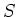 .
This holds even if
.
This holds even if 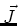 is not uniform over the surface
is not uniform over the surface 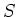 , i.e. if
, i.e. if
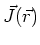 varies from point to point on
varies from point to point on 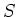 .
.
=2.0 true in
Microscopically, the current density is the product of
the amount of charge per unit volume and how fast the charge is moving:
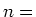 number of charge carriers per unit volume
number of charge carriers per unit volume
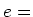 charge of each carrier (usually they are electrons)
charge of each carrier (usually they are electrons)
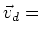 ``drift" velocity of charge density
``drift" velocity of charge density
Derivation: A piece of wire of length 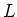 and cross sectional area
and cross sectional area 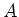 has charge.
has charge.
=2.0 true in
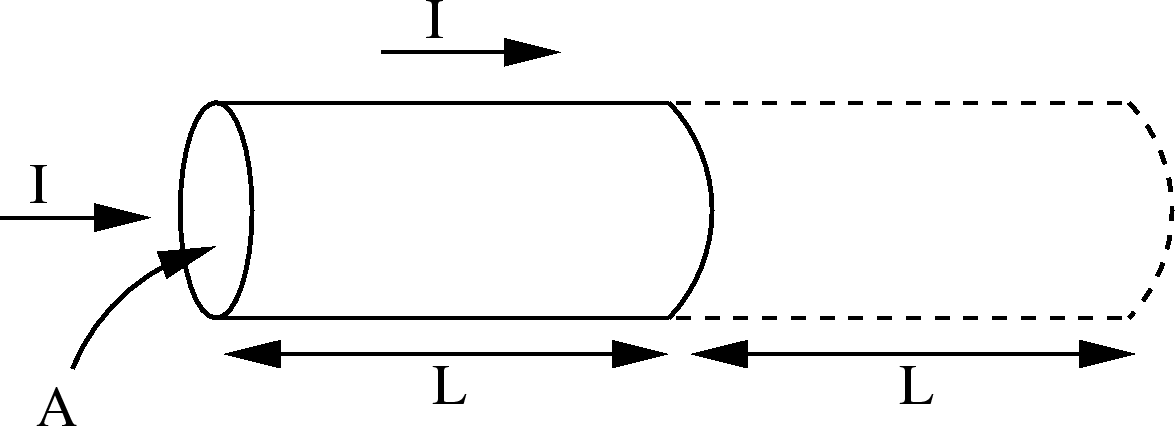
It takes a time 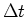 for this charge to completely leave this volume:
for this charge to completely leave this volume:
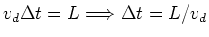 .
In time
.
In time 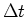 each charge carrier has migrated a distance
each charge carrier has migrated a distance 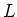 .
.
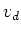 is not the velocity of the electrons. Typically the electron velocity
is not the velocity of the electrons. Typically the electron velocity
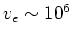 m/s. But the electrons hit things like atoms,
impurities, and imperfections in the conductor. This gives rise to
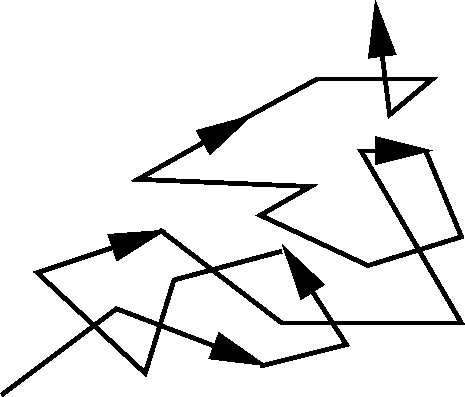
resistance. So the electrons don't travel ballistically (in
straight lines). They bounce around and make slow progress down the wire.
m/s. But the electrons hit things like atoms,
impurities, and imperfections in the conductor. This gives rise to
resistance. So the electrons don't travel ballistically (in
straight lines). They bounce around and make slow progress down the wire.
is due to electrons hitting things.
=1.0 true in
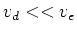 . Typically
. Typically
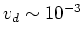 m/s. (If you bounce off the walls, it takes longer to get out of the
room.)
m/s. (If you bounce off the walls, it takes longer to get out of the
room.)
It doesn't take long for the light to go on when you flip a switch for the same
reason that it doesn't take long for water come out of a hose when you turn on
the faucet. There's already water in the hose. Similarly there are
electrons in
the wire, and they all start to drift when you flip the switch.
Resistance
The ratio of voltage over current is .
If we apply a voltage 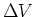 across the ends of a conductor (or wire),
a current
across the ends of a conductor (or wire),
a current 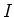 flows. The ratio
flows. The ratio 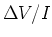 is called
the resistance
is called
the resistance 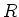 :
:
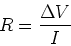 |
(3) |
If 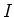 is big,
is big,
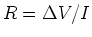 is small
is small
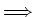 small resistance
means big current. If
small resistance
means big current. If  is small
is small
 large resistance.
large resistance.
Units
The unit of resistance is the .
Ohm's law is .
If 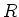 = constant independent of
= constant independent of 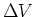 or
or 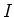 , then the current
, then the current 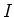 flowing through a device is directly proportional to the potential difference
flowing through a device is directly proportional to the potential difference
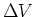 across
the device:
across
the device:
This is called Ohm's Law.
=2.0 true in
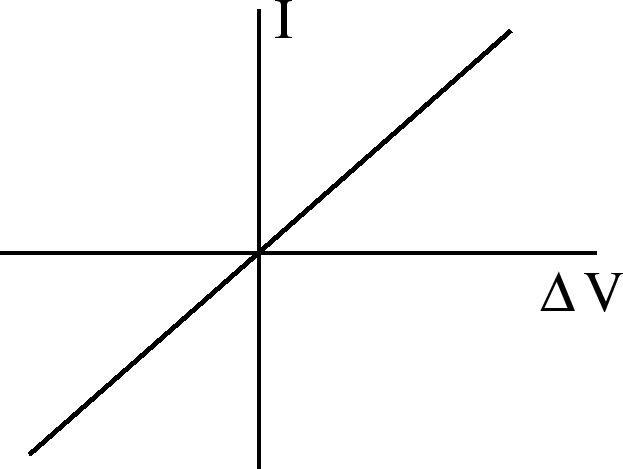
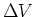 :
:
=2.0 true in
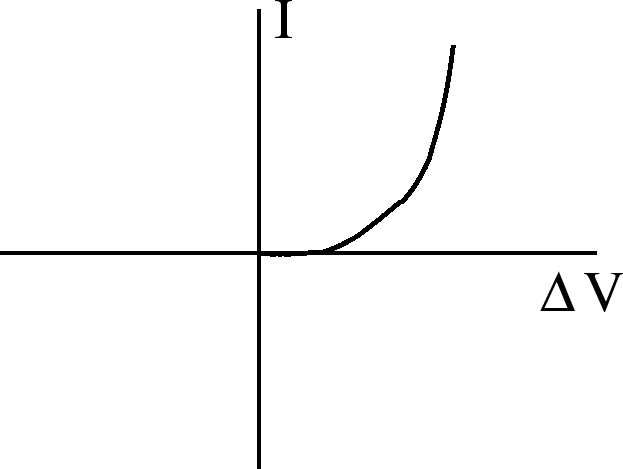
Resistivity
Sometimes it is more convenient to think in terms of 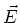 and
and 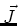 at
a point in the conductor, rather than the voltage drop
at
a point in the conductor, rather than the voltage drop 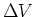 across a conductor and the current
across a conductor and the current 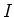 flowing through it. In this case
we define the resistivity
flowing through it. In this case
we define the resistivity
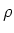 to be the ratio
to be the ratio 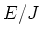 . Here we are assuming that
. Here we are assuming that 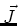 points in the direction of
points in the direction of 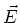 . (That's how we defined the direction of
. (That's how we defined the direction of
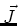 .)
.)
Units:
![$[\rho] = \left[\frac{E}{J}\right] =
\frac{V/m}{A/m^{2}} = V \cdot m/A = \Omega \cdot m $](img68.png) which is called an
``ohm-meter".
which is called an
``ohm-meter".
Vector form:
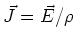
is the inverse of resistivity.
We can define the conductivity:
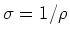 . Then
. Then
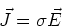 |
(4) |
Units:
![$[\sigma] = (\Omega \cdot m)^{-1}$](img72.png) which is called
``reciprocal ohm-meter" or ``inverse ohm-meter" or ``mhos per meter".
which is called
``reciprocal ohm-meter" or ``inverse ohm-meter" or ``mhos per meter".
depends on the material, not on its size or geometry.
Resistivity is a property of the material, not its dimensions. Resistance
depends on the material and the dimensions of the resistor. A
resistor is a conductor with a specified resistance, e.g., 100  .
You put resistors in circuits. They are denoted in circuit diagrams
by a wiggly line.
.
You put resistors in circuits. They are denoted in circuit diagrams
by a wiggly line.
=1.0 true in
Resistance is proportional to times length, and
inversely proportional to area.
Consider a resistive wire segment of cross-sectional area 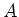 , length
, length 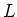 ,
with a voltage drop
,
with a voltage drop 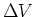 across it. Assume
across it. Assume 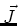 and
and 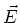 are constant everywhere within the wire.
are constant everywhere within the wire.
=3.0 true in
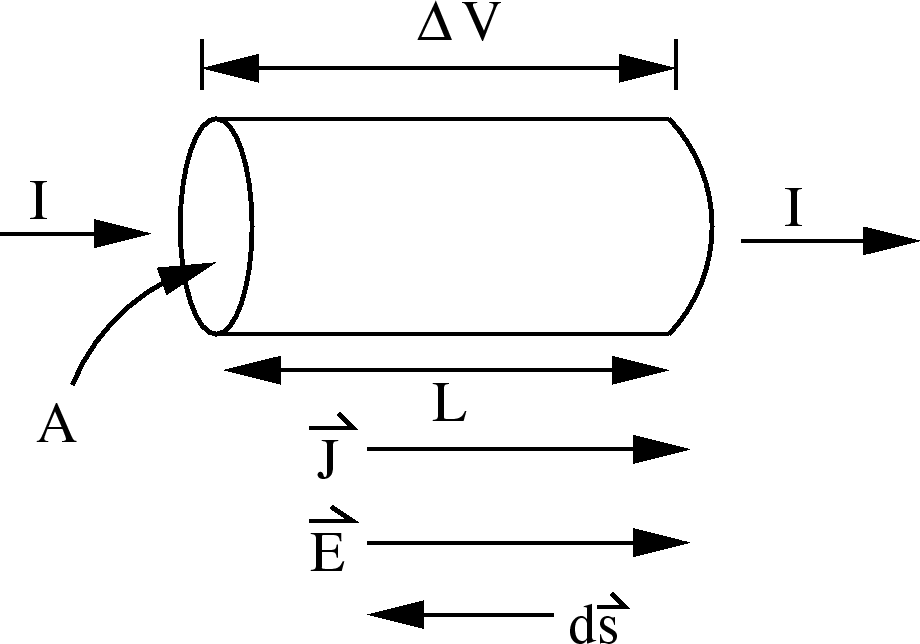
We can check this by going backwards:
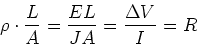 |
(6) |
To understand why this formula makes sense, we need to realize that resistance
results from electrons bumping into things (atoms, impurities, imperfections,
the walls of the wire) as they travel down the wire. The longer the wire is,
the more things there are to bump into
 .
The thicker
the wire is, the easier it is to go around the road blocks
.
The thicker
the wire is, the easier it is to go around the road blocks
 Area. So
Area. So 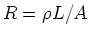
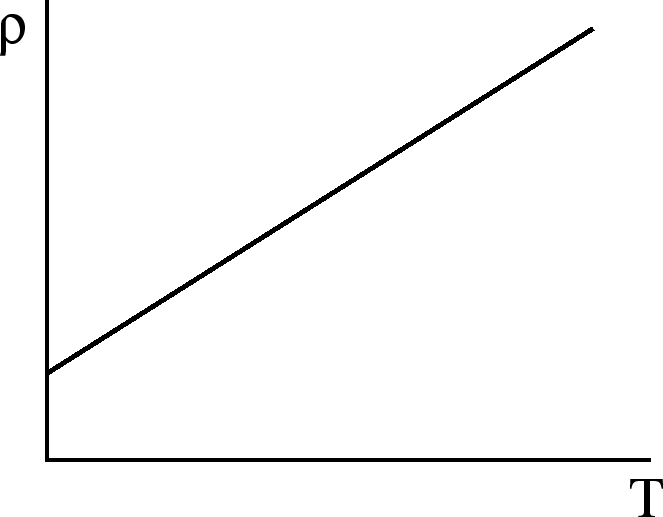
Note that 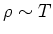 , because the hotter the wire is, the more the atoms
vibrate, the harder it is for electrons to get by jostling atoms. Your
book gives the formula
, because the hotter the wire is, the more the atoms
vibrate, the harder it is for electrons to get by jostling atoms. Your
book gives the formula
![$\rho=\rho_o[1+\alpha(T-T_o)]$](img87.png) .
.
=2.0 true in
Power Dissipation
Resistance leads to .
Suppose there is a voltage drop across some circuit element or device, e.g., a
light bulb, a resistor, a motor, etc.
=2.0 true in
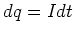 moves through
that potential drop
moves through
that potential drop 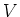 , it gives up potential energy
, it gives up potential energy 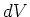
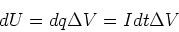 |
(7) |
This is like a ball falling down - it loses potential energy and gains kinetic
energy. The potential energy lost by the charge is converted into some other
form of energy, e.g. heat, light, work, etc. The rate of energy transfer is
called power 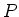 .
.
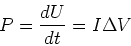 |
(8) |
Units:
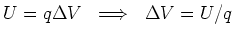
![$[P] =$](img97.png) Volts
Volts 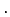 Amperes = (1 J/C) (1 C/s) = 1 J/s = 1 W.
Amperes = (1 J/C) (1 C/s) = 1 J/s = 1 W.
If we have a resistor
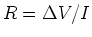 , then
, then 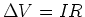 .
Using this, we can write:
.
Using this, we can write:
These formulas describe power dissipation in a resistor.
Note: A light bulb burns out when you first turn it on because the filament
(i.e., the resistor) is cold and its resistance is low. Hence the power
dissipated
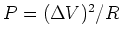 is high and the filament burns out.
is high and the filament burns out.
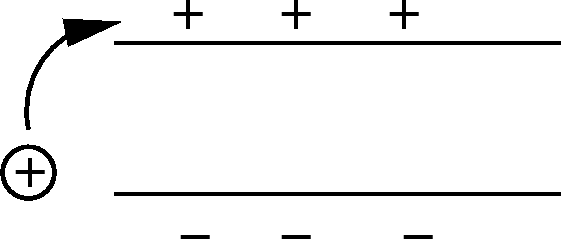
Emf
The amount of work done per unit charge is called the .
Recall that when a battery charges a capacitor, it takes  charge from the
negatively charged plate and puts it on the positively charged plate.
We can think of the battery as a charge pump. It does work.
charge from the
negatively charged plate and puts it on the positively charged plate.
We can think of the battery as a charge pump. It does work.
=2.0 true in
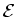 ("electromotive force"):
("electromotive force"):
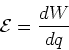 |
(9) |
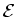 is a scalar.
The battery is an example of an emf device. Emf devices are
charge pumps. They provide emf, i.e., they do work. Other
examples: electric generators, solar cells, etc. The gravitational
analogy of a battery is an escalator or an elevator that goes up.
is a scalar.
The battery is an example of an emf device. Emf devices are
charge pumps. They provide emf, i.e., they do work. Other
examples: electric generators, solar cells, etc. The gravitational
analogy of a battery is an escalator or an elevator that goes up.
Units: [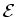 ] = Joule/ Coulomb = Volt. (e.g. 12V battery)
] = Joule/ Coulomb = Volt. (e.g. 12V battery)
Gravitational analogy: The work done per unit mass in lifting a weight is the
analog of emf 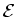 . The potential energy per unit mass that
the mass gains is the analog of electric potential. The difference
between
. The potential energy per unit mass that
the mass gains is the analog of electric potential. The difference
between 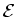 and
and 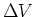 is like the difference between going uphill
and being able to roll downhill.
is like the difference between going uphill
and being able to roll downhill.
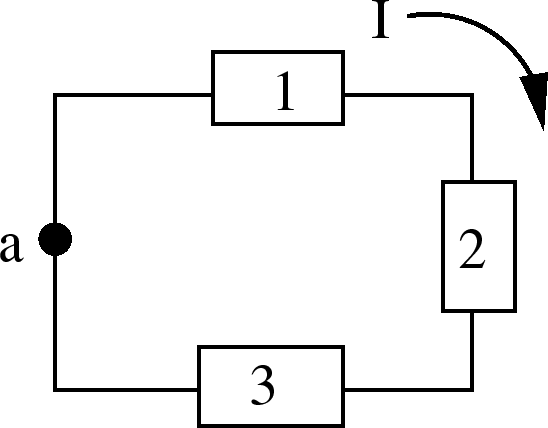
Calculating Current
To show that 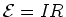 , we can use a technique that is useful
in analyzing circuits.
Potential Around a Loop
, we can use a technique that is useful
in analyzing circuits.
Potential Around a Loop
In the rule, sum the changes in potential
in going around a loop of the circuit.
If we start at a point in the circuit which has potential 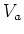 , then go
around the circuit adding and subtracting voltages as we meet different circuit
elements, and finally return to pt. A, our voltage must again be
, then go
around the circuit adding and subtracting voltages as we meet different circuit
elements, and finally return to pt. A, our voltage must again be
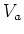 . Thus, all those voltage differences must sum to zero.
. Thus, all those voltage differences must sum to zero.
=2.0 true in
This is called the loop rule: The algebraic sum of the changes in
potential encountered in a complete transversal of any circuit must be zero.
The loop rule is the other Kirchhoff rule. Kirchhoff's rules are used
in analyzing circuits.
=2.0 true in
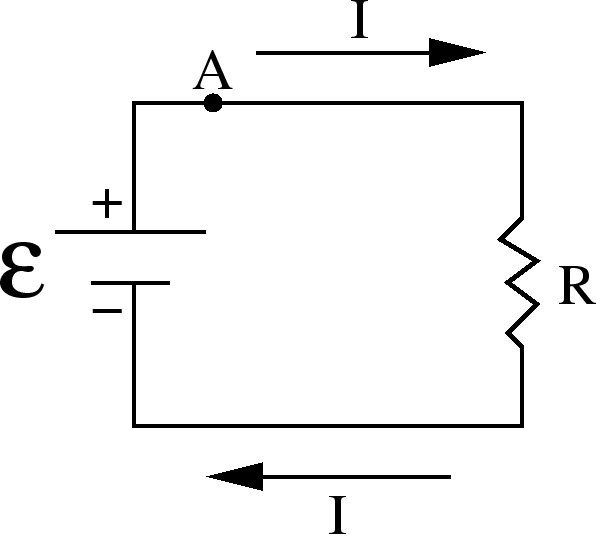
Recipe for Analyzing Circuits
- Choose the directions of the currents in each segment or section
of the circuit. Sometimes we may not know the true direction of the
current
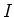 . Just guess a direction for
. Just guess a direction for 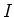 , and adhere to the resistance
rule. If you choose wrong, you will find
, and adhere to the resistance
rule. If you choose wrong, you will find 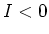 which means the current
goes in the opposite direction from your choice.
which means the current
goes in the opposite direction from your choice.
- Choose the direction in which you mentally go around each loop
in the circuit.
- Use the loop rule to write down equations. Keep the following in
mind:
- Resistance Rule:
If you mentally pass through
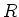 in the direction of the current
in the direction of the current 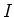 , the
potential decreases by
, the
potential decreases by 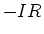 . This is like going downhill. If you go against
the current through
. This is like going downhill. If you go against
the current through 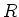 , you gain potential
, you gain potential 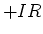 . This is like going uphill.
. This is like going uphill.
- EMF Rule:
If you mentally pass through an ideal emf device
from
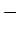 to
to 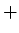 , then you gain potential
, then you gain potential 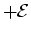 . If you go in
the opposite direction, you lose potential
. If you go in
the opposite direction, you lose potential 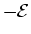 .
.
- Use the junction rule to help write down equations.
Sometimes we meet junctions or branches in circuits. In this case,
we apply the junction rule:
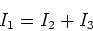 |
(10) |
=1.0 true in
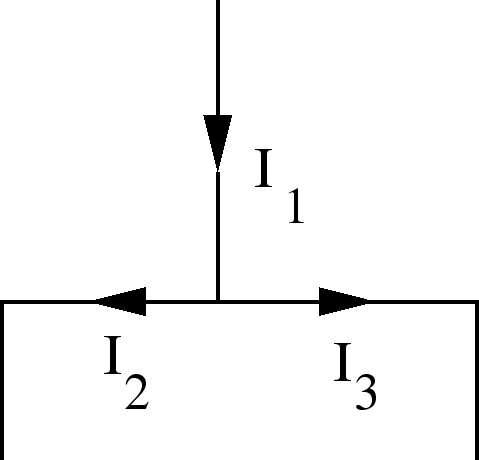
Kirchhoff's rules are the loop rule and the junction rule.
We will use these rules to understand how to treat resistors in circuits.
Resistors in Series
resistances in series to find the equivalent
resistance.
An example of resistance in series is resistors that
come one right after the other
like a string of Christmas tree lights. Connected resistances are
said to be in series when the potential difference applied across
the combination is the sum of
the resulting differences across the individual resistances.
=2.0 true in
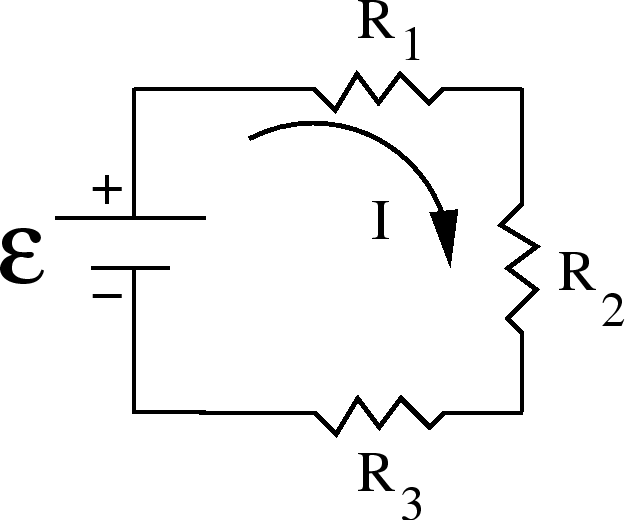
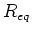 that is equivalent to
that is equivalent to
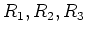 .
.
=2.0 true in
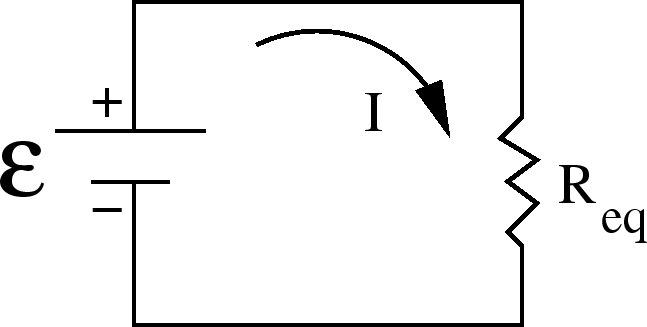
To do this apply the loop rule and go around the
circuit:
where
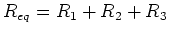
In general one adds resistances in series to get an equivalent resistance:
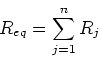 |
(12) |
where 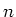 is the number of resistors in series.
In the book, ``real'' emf devices have a resistance
is the number of resistors in series.
In the book, ``real'' emf devices have a resistance 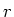 in series with an
ideal emf device. An ideal emf device has no resistance.
in series with an
ideal emf device. An ideal emf device has no resistance.
=3.0 true in
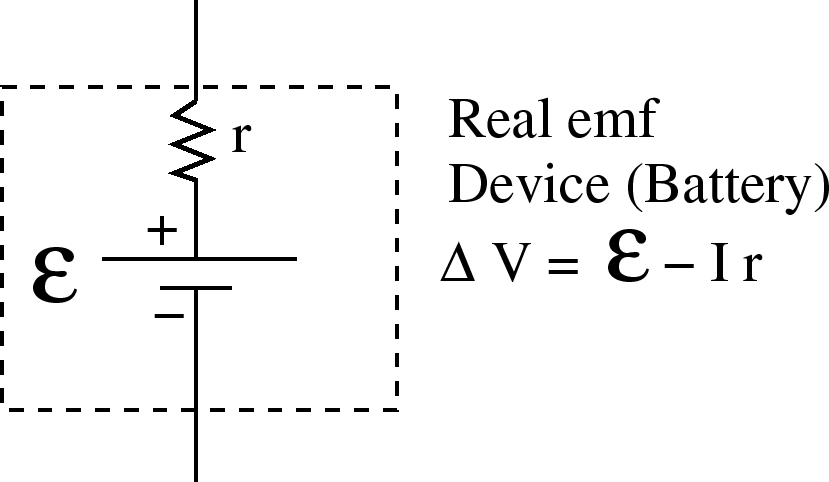
A voltage divider consists of 2 (or more) resistors in series:
=3.0 true in
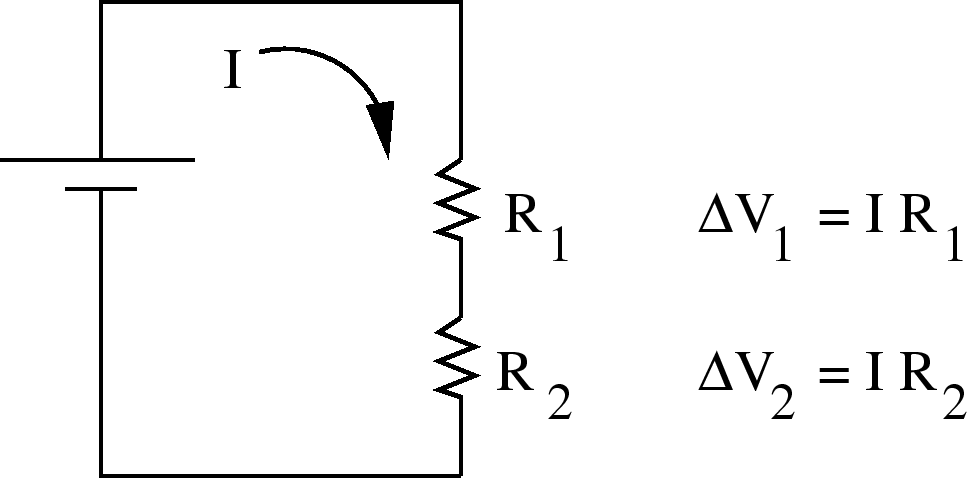
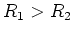 ,
,
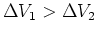 .
.
Potential Differences
To find the potential difference between two points in a circuit, start at one
point and transverse the circuit to the other, following any path, and add
algebraically the changes in potential that you encounter. Recall that the
potential difference 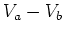 between two points is independent of the
path you take between them.
between two points is independent of the
path you take between them.
=2.0 true in
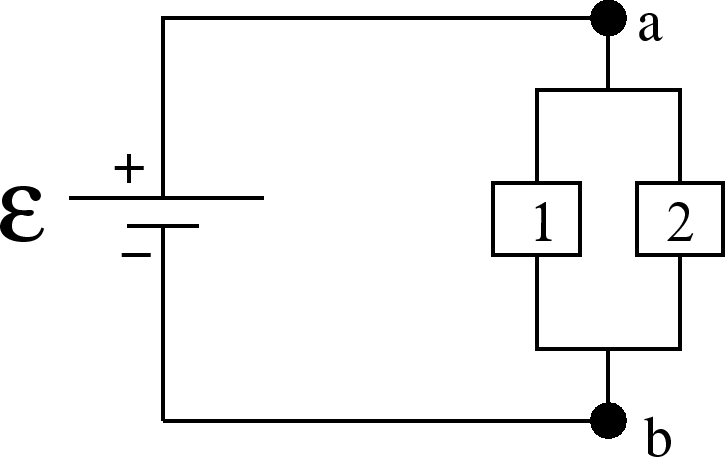
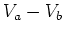 is the same whether you go through 1 or through 2.
is the same whether you go through 1 or through 2.
Resistances in Parallel
To find the equivalent resistance for resistors in parallel, sum the resistances.
An example of 2 resistances in parallel is:
=2.0 true in
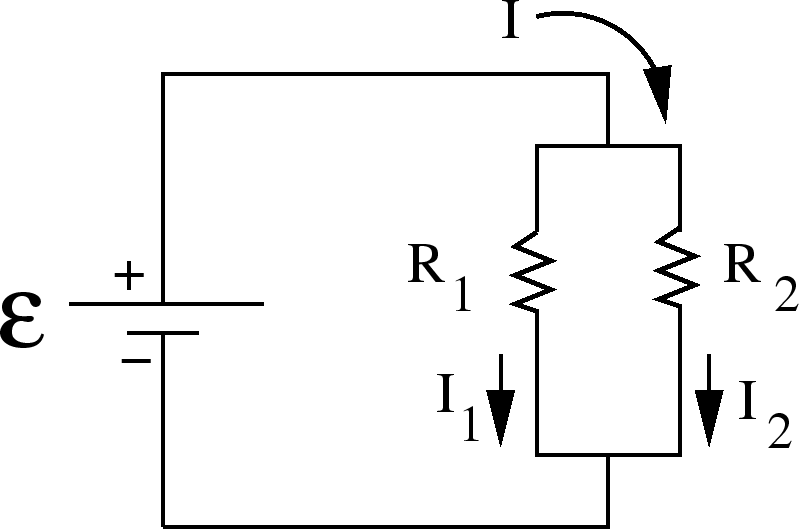
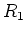 is the same as that across
is the same as that across 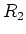 :
:
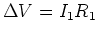 and
and
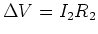 .
.
To find an equivalent resistance 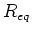 that can replace
that can replace 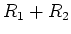 without changing the current
without changing the current 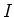 through the combination or the voltage
through the combination or the voltage
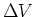 across it, we note that the junction rule tells us
across it, we note that the junction rule tells us
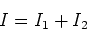 |
(13) |
where
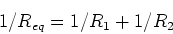 |
(15) |
In general we add inverse resistances when they are in parallel:
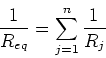 |
(16) |
where there are 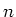 resistances in parallel.
resistances in parallel.
Comparison of resistors and capacitors:
Series Parallel
Resistors
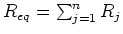
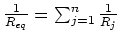
Capacitors

Note that we can rearrange circuits to topologically equivalent conformations
because wires are equipotentials. Here are some examples:
=3.0 true in
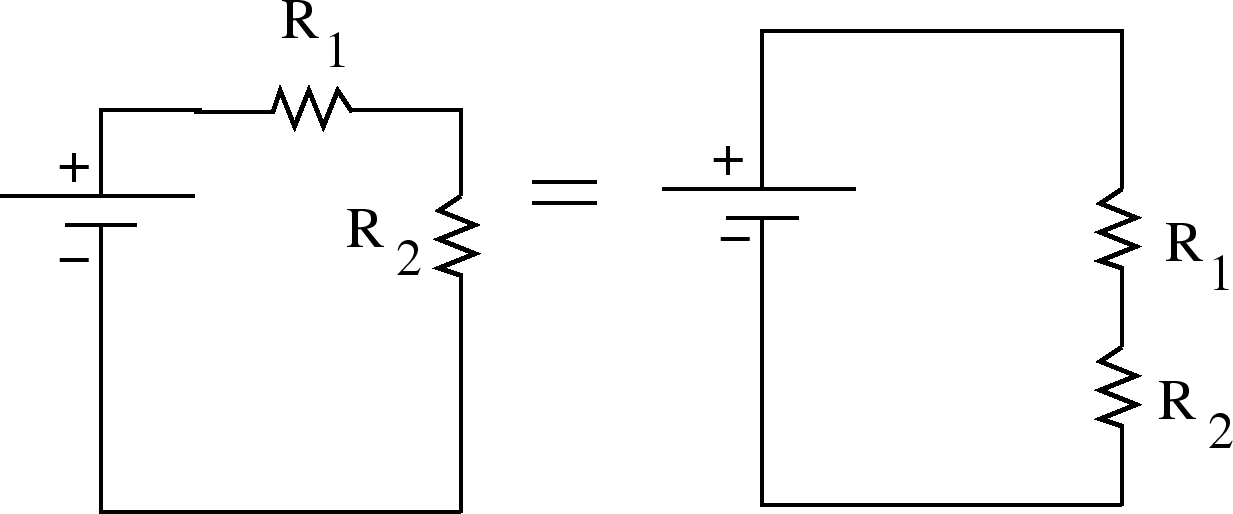
=3.0 true in
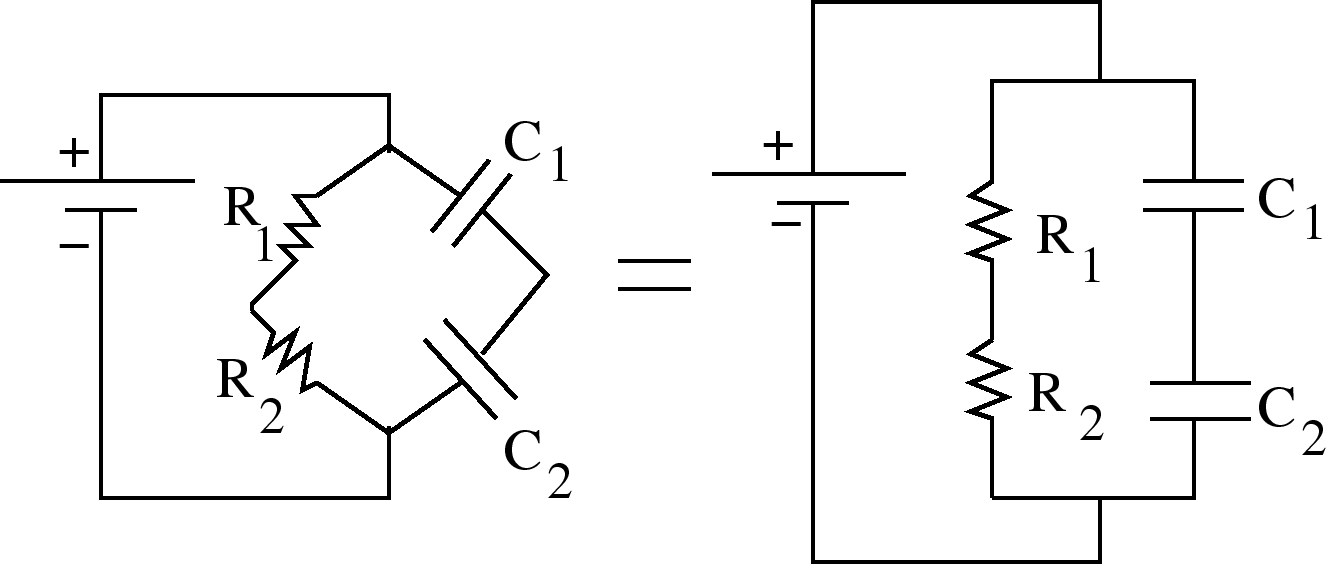
Example: Problem 21.30
Three 100 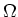 resistors are connected as shown. The maximum
power that can safely be delivered to any one resistor is 25.0 W. (a)
What is the maximum voltage that can be applied to the terminals
resistors are connected as shown. The maximum
power that can safely be delivered to any one resistor is 25.0 W. (a)
What is the maximum voltage that can be applied to the terminals 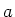 and
and 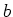 ? (b) For the voltage determined in part (a), what is the
power delivered to each resistor? What is the total power delivered?
? (b) For the voltage determined in part (a), what is the
power delivered to each resistor? What is the total power delivered?
=3.0 true in
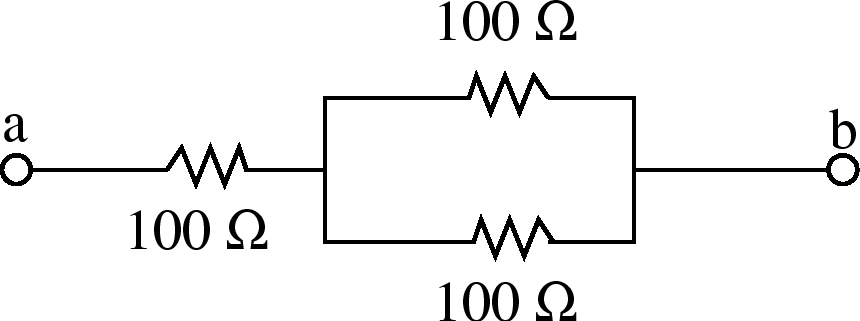
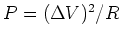 . So the voltage drop across the resistor is
. So the voltage drop across the resistor is
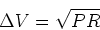 |
(17) |
We need to find which resistor will
have the most power dissipated. It will be the resistor with
the biggest voltage drop. First let's find the equivalent resistance 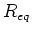 for the resistors in parallel. The resistors all have the same resistance.
Let
for the resistors in parallel. The resistors all have the same resistance.
Let
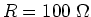 . Then
. Then
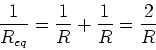 |
(18) |
or 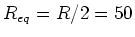
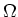 . So now our circuit looks like
. So now our circuit looks like
=3.0 true in
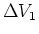 across
across
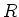 is
is 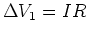 and the voltage drop across
and the voltage drop across
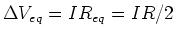 . So
. So
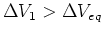 . In fact
. In fact
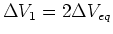 .
So the power dissipated in
.
So the power dissipated in 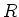 will be greater than the power dissipated
in
will be greater than the power dissipated
in 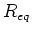 . The maximum power that can be dissipated in a resistor is
25 W. So this is the power dissipated in the first resistor. The voltage
drop across
. The maximum power that can be dissipated in a resistor is
25 W. So this is the power dissipated in the first resistor. The voltage
drop across 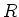 is given by eq. (19):
is given by eq. (19):
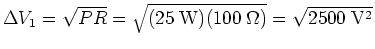 = 50 V. The current through the resistor is
= 50 V. The current through the resistor is
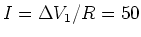 V/100
V/100
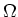 = 0.5 A. The voltage drop from
= 0.5 A. The voltage drop from 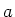 to
to 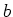 is
is
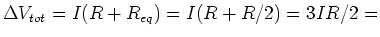 3(100
3(100 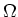 )(0.5 A)/2 = 75 V.
)(0.5 A)/2 = 75 V.
(b) The power delivered to the first resistor is 25 W as we found in
part a. Each resistor in parallel will have 1/2 the current going through
it. So the power dissipated in each resistor in parallel is
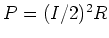 = (0.5 A/2)
= (0.5 A/2)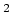 (100
(100 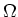 )= 6.25 W. The total power
delivered is the sum of the power dissipated in each resistor:
)= 6.25 W. The total power
delivered is the sum of the power dissipated in each resistor:
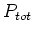 = 25 W + 6.25 W + 6.25 W = 37.5 W.
= 25 W + 6.25 W + 6.25 W = 37.5 W.
RC circuits
In an RC circuit with a capacitor and resistor in series, the characteristic
time to charge or discharge the capacitor is .
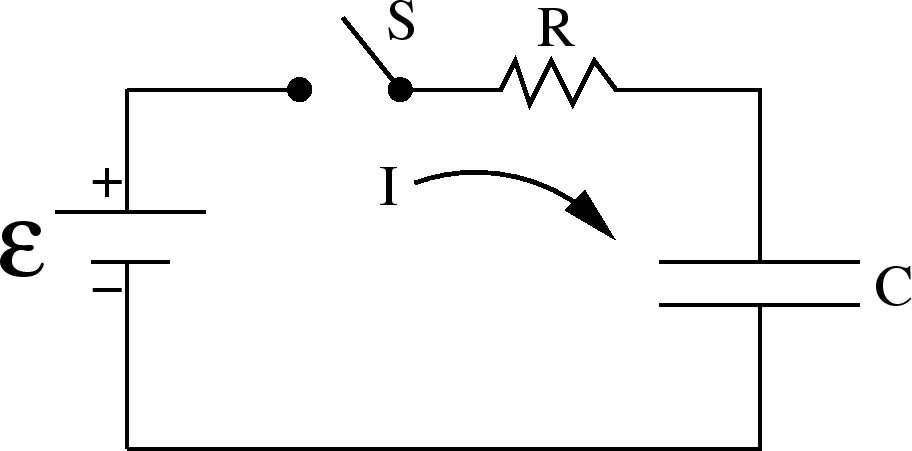
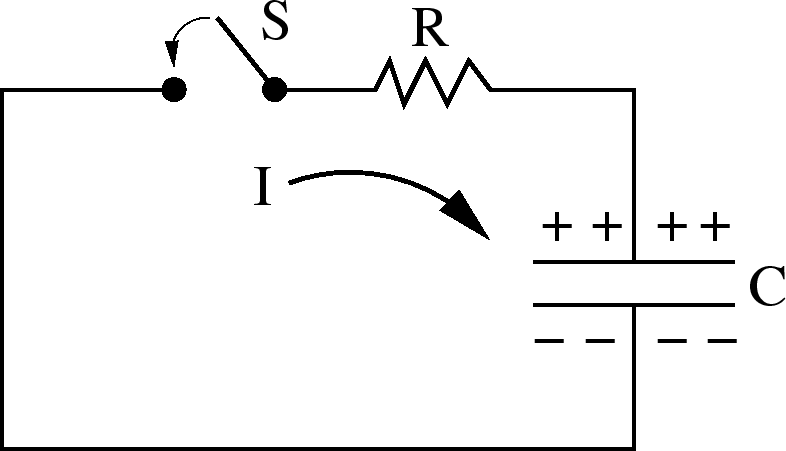
Charging a capacitor: Suppose the capacitor
is initially uncharged. Then there is no voltage drop
across it. When we close the switch, current starts to
flow and the capacitor begins to charge up.
=2.0 true in
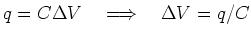 )
)
Going from the positively charged plate to the
negatively charged plate in the direction of the current
corresponds to a voltage drop,
=1.4 true in
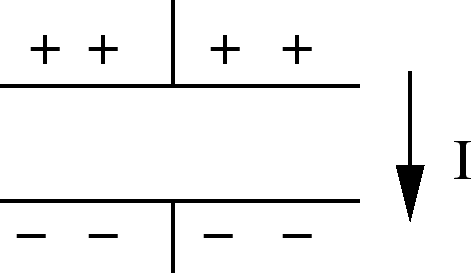
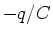 . We rewrite the equation
. We rewrite the equation
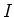 and
and 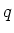 are related by
are related by 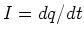 . Plugging this in yields
. Plugging this in yields
This is a 1st order linear differential equation for 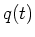 . The
initial condition is
. The
initial condition is 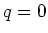 at
at 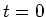 . Initially, when
. Initially, when 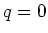 ,
there is no voltage drop across
,
there is no voltage drop across 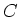 , so we have
, so we have
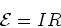 |
(19) |
As the charge 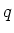 on the capacitor increases with time,
on the capacitor increases with time, 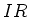 becomes
less important, i.e. the current decreases. Eventually, when the
capacitor is fully charged
becomes
less important, i.e. the current decreases. Eventually, when the
capacitor is fully charged
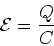 |
(20) |
and 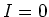 , i.e., current doesn't flow. Here
, i.e., current doesn't flow. Here 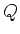 is the maximum
charge on the capacitor.
So we want to solve:
is the maximum
charge on the capacitor.
So we want to solve:
We can rearrange the terms with 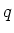 on one side and
on one side and 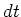 on the other:
on the other:
Exponentiating both sides leads to
where 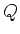 is the maximum charge on the capacitor. This comes from
eq. (22) which applies when the capacitor is fully charged
and the potential drop across
is the maximum charge on the capacitor. This comes from
eq. (22) which applies when the capacitor is fully charged
and the potential drop across 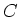 is the emf
is the emf 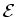 of the battery.
Notice that at
of the battery.
Notice that at 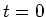 ,
,
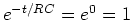 ,
,
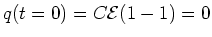 as
desired. At
as
desired. At 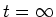 ,
,
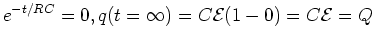 or
or
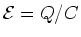 as desired.
as desired.
The current
![\begin{displaymath}
I = \frac{dq}{dt} = \frac{d}{dt} \left[ C{\cal E} (1-e^{-t/RC})\right] =
\frac{\cal E}{R} e^{-t/RC}
\end{displaymath}](img209.png) |
(21) |
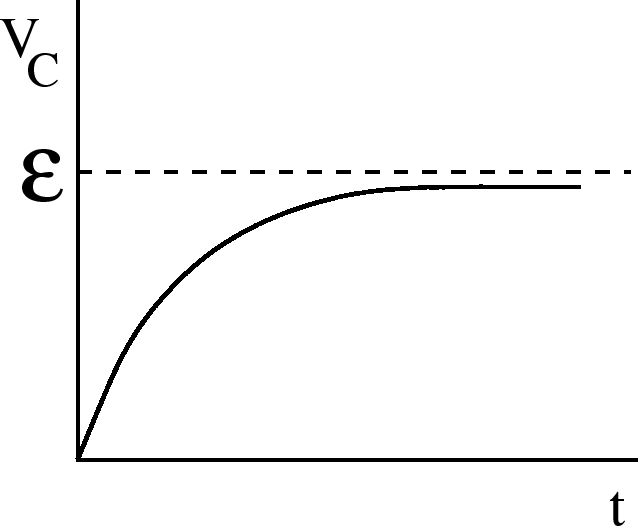
So at 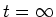 ,
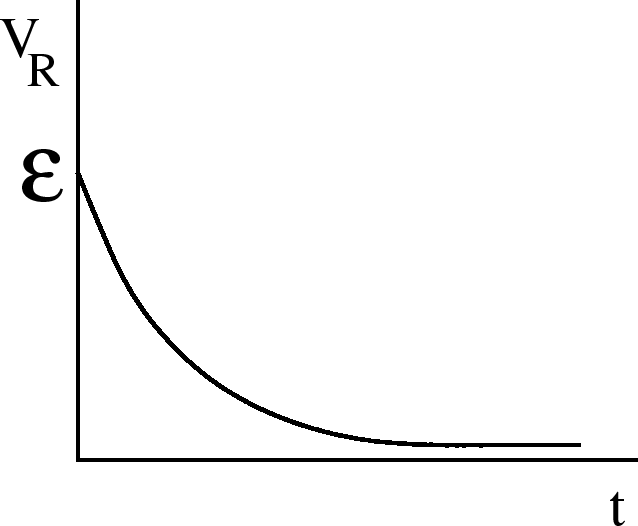
, 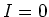 . The voltage across the capacitor
. The voltage across the capacitor
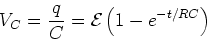 |
(22) |
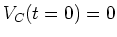 .
.
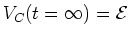 .
.
=2.0 true in
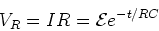 |
(23) |
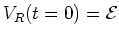 .
.
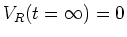 .
.
=2.0 true in
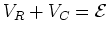 at all times.
at all times.
The time constant: In the exponent of 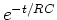 ,
, 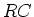 has
units of time because the exponent
has
units of time because the exponent 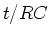 must be dimensionless.
must be dimensionless.
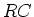 is called the time constant of the circuit. It is often
denoted by
is called the time constant of the circuit. It is often
denoted by 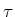 , i.e.,
, i.e., 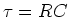 . It is the
characteristic time involved in charging the capacitor, i.e. it sets
the time scale. When
. It is the
characteristic time involved in charging the capacitor, i.e. it sets
the time scale. When 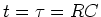 ,
,
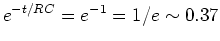 . So
. So
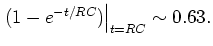 So when
So when 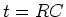 , the capacitor is charged up to 63% of being fully charged.
, the capacitor is charged up to 63% of being fully charged.
Discharging a capacitor
Suppose the capacitor is fully charged with charge 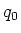 .
.
=1.25 true in
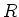 by closing
the switch in the circuit shown.
Since
by closing
the switch in the circuit shown.
Since 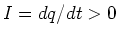 , this implies that
, this implies that 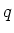 increases as
time increases. In particular, the direction of
increases as
time increases. In particular, the direction of 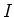 should be such
that the charge on the capacitor increases with time, i.e.,
should be such
that the charge on the capacitor increases with time, i.e., 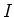 flows
toward the positively charged plate.
flows
toward the positively charged plate.
=2.0 true in
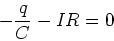 |
(24) |
One way to get this is to
set 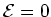 in the charging equation
in the charging equation
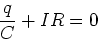 |
(25) |
Plug in 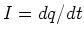 to get
to get
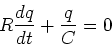 |
(26) |
Solution:
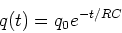 |
(27) |
Discharging capacitor:
At characteristic time 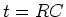 ,
,
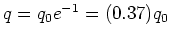 . So only
37% of the original charge remains on the capacitor at
. So only
37% of the original charge remains on the capacitor at 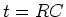 .
.
Current during discharge:
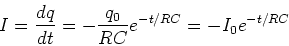 |
(28) |
where
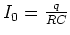 .
The minus sign indicates that the discharging current is in
the opposite direction from the charging current.
.
The minus sign indicates that the discharging current is in
the opposite direction from the charging current.



Next: About this document ...
Clare Yu
2007-02-19


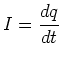
![]() is the amount of
charge passing through the plane in the time interval from
is the amount of
charge passing through the plane in the time interval from ![]() to
to ![]() .
.

![]() (amperes = "amp").
(amperes = "amp").

![]() ] = Ampere/m
] = Ampere/m![]()
![]() is a vector that points in the direction of
is a vector that points in the direction of ![]() . (We need
. (We need
![]() to make current flow.) The total current
to make current flow.) The total current ![]() through a
surface
through a
surface ![]() is
is

![]() and cross sectional area
and cross sectional area ![]() has charge.
has charge.

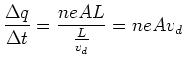
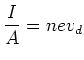

![]()
![]() across the ends of a conductor (or wire),
a current
across the ends of a conductor (or wire),
a current ![]() flows. The ratio
flows. The ratio ![]() is called
the resistance
is called
the resistance ![]() :
:
![$\displaystyle 1 \Omega = 1 \frac{\rm {volt}}{\rm {ampere}} = 1 \frac{V}{A}
= \left[\frac{\Delta V}{I}\right]$](img61.png)
![]() = constant independent of
= constant independent of ![]() or
or ![]() , then the current
, then the current ![]() flowing through a device is directly proportional to the potential difference
flowing through a device is directly proportional to the potential difference
![]() across
the device:
across
the device:
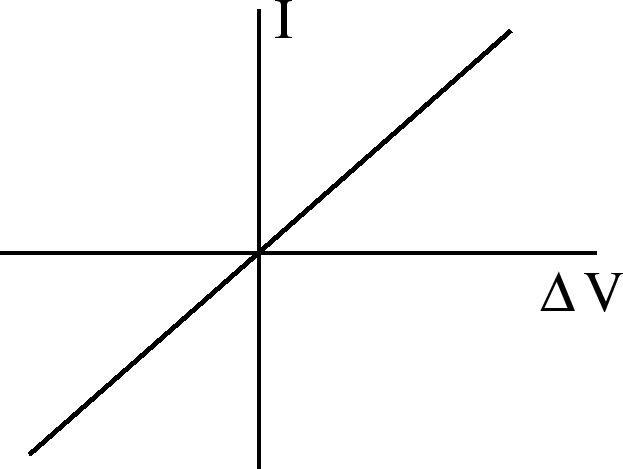
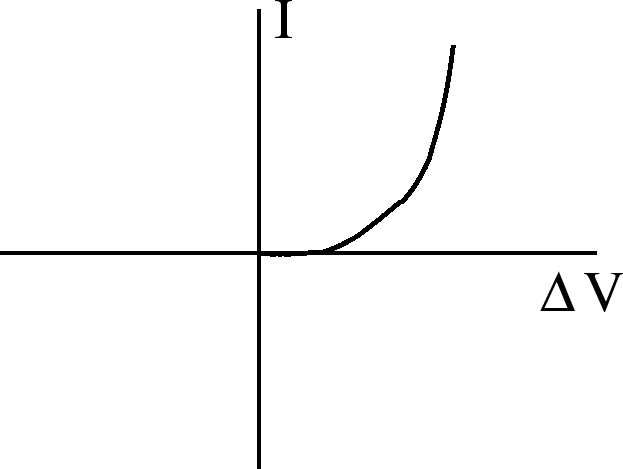
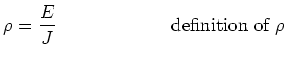
![]() which is called an
``ohm-meter".
which is called an
``ohm-meter".
![]()
![]() . Then
. Then
![]() .
You put resistors in circuits. They are denoted in circuit diagrams
by a wiggly line.
.
You put resistors in circuits. They are denoted in circuit diagrams
by a wiggly line.
![]() , length
, length ![]() ,
with a voltage drop
,
with a voltage drop ![]() across it. Assume
across it. Assume ![]() and
and ![]() are constant everywhere within the wire.
are constant everywhere within the wire.

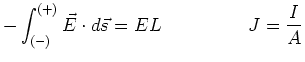
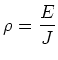
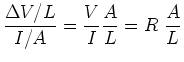
![]() , because the hotter the wire is, the more the atoms
vibrate, the harder it is for electrons to get by jostling atoms. Your
book gives the formula
, because the hotter the wire is, the more the atoms
vibrate, the harder it is for electrons to get by jostling atoms. Your
book gives the formula
![]() .
.


![]() , then
, then ![]() .
Using this, we can write:
.
Using this, we can write:
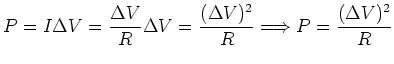
![]() is high and the filament burns out.
is high and the filament burns out.
![]() charge from the
negatively charged plate and puts it on the positively charged plate.
We can think of the battery as a charge pump. It does work.
charge from the
negatively charged plate and puts it on the positively charged plate.
We can think of the battery as a charge pump. It does work.

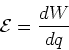
![]() ] = Joule/ Coulomb = Volt. (e.g. 12V battery)
] = Joule/ Coulomb = Volt. (e.g. 12V battery)
![]() . The potential energy per unit mass that
the mass gains is the analog of electric potential. The difference
between
. The potential energy per unit mass that
the mass gains is the analog of electric potential. The difference
between ![]() and
and ![]() is like the difference between going uphill
and being able to roll downhill.
is like the difference between going uphill
and being able to roll downhill.
![]() , then go
around the circuit adding and subtracting voltages as we meet different circuit
elements, and finally return to pt. A, our voltage must again be
, then go
around the circuit adding and subtracting voltages as we meet different circuit
elements, and finally return to pt. A, our voltage must again be
![]() . Thus, all those voltage differences must sum to zero.
. Thus, all those voltage differences must sum to zero.


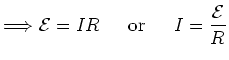


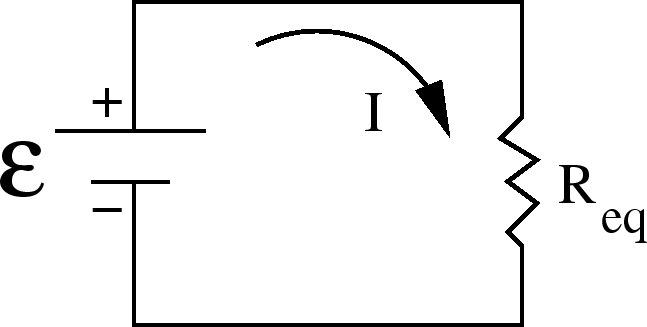
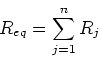




![]() that can replace
that can replace ![]() without changing the current
without changing the current ![]() through the combination or the voltage
through the combination or the voltage
![]() across it, we note that the junction rule tells us
across it, we note that the junction rule tells us
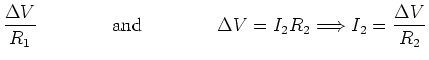
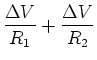
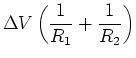
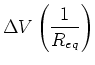
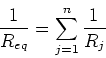
![]()
![]()
![]()
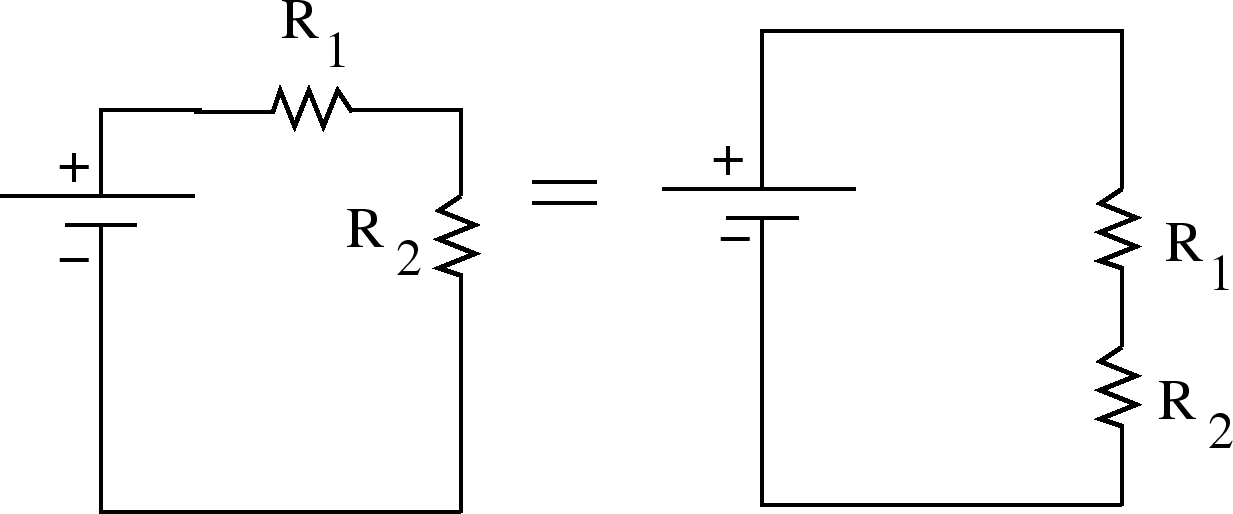
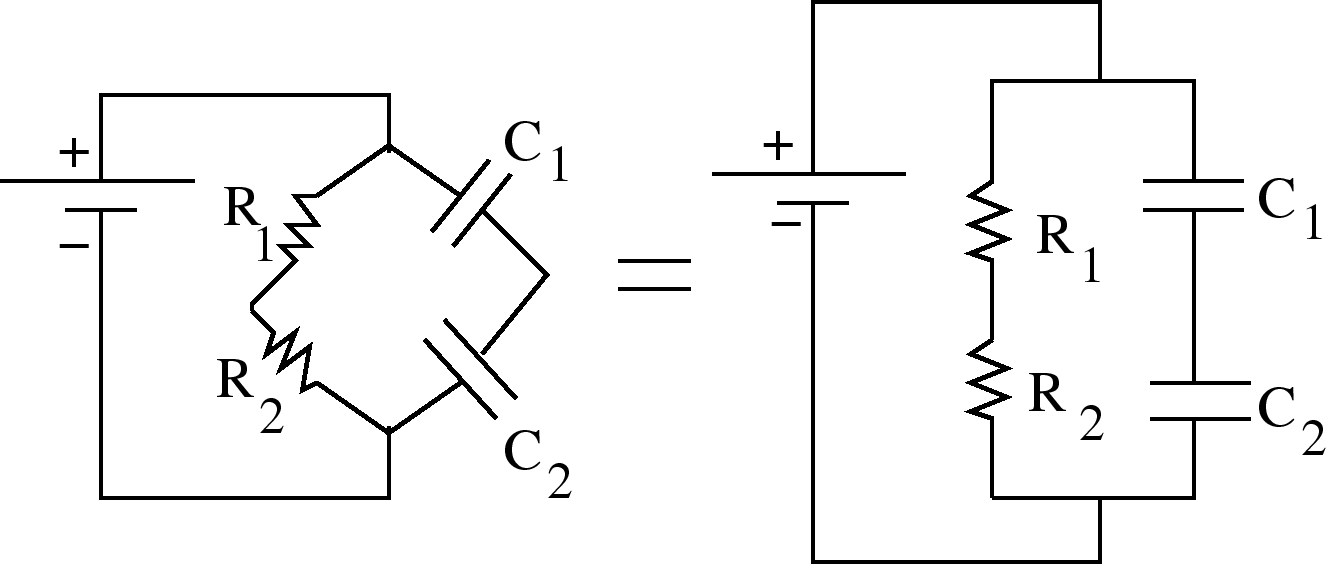

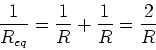
![]() = (0.5 A/2)
= (0.5 A/2)![]() (100
(100 ![]() )= 6.25 W. The total power
delivered is the sum of the power dissipated in each resistor:
)= 6.25 W. The total power
delivered is the sum of the power dissipated in each resistor:
![]() = 25 W + 6.25 W + 6.25 W = 37.5 W.
= 25 W + 6.25 W + 6.25 W = 37.5 W.

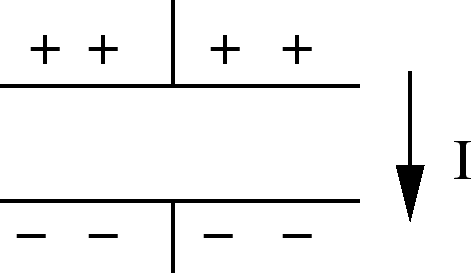
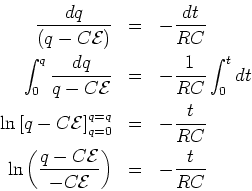
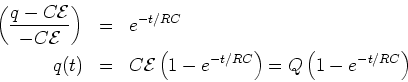


![]() ,
, ![]() has
units of time because the exponent
has
units of time because the exponent ![]() must be dimensionless.
must be dimensionless.
![]() is called the time constant of the circuit. It is often
denoted by
is called the time constant of the circuit. It is often
denoted by ![]() , i.e.,
, i.e., ![]() . It is the
characteristic time involved in charging the capacitor, i.e. it sets
the time scale. When
. It is the
characteristic time involved in charging the capacitor, i.e. it sets
the time scale. When ![]() ,
,
![]() . So
. So
![]() So when
So when ![]() , the capacitor is charged up to 63% of being fully charged.
, the capacitor is charged up to 63% of being fully charged.