


Next: About this document ...
LECTURE 8
How a Laser Works
Laser is an acroynm that stands for Light Amplification by Stimulated
Emission of Radiation. A maser is the corresponding system for
microwaves. To understand how a laser works, consider an atom
with 2 energy levels and one electron.
Let's call this a two level system. Let E1 be
the energy of the ground state and E2 be the energy of
the excited state. Suppose the electron is in the lower energy
state. If the atom absorbs a photon of frequency
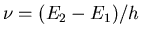 ,
the electron makes a transition to the excited state. From there it
can decay back to the lower state by emitting a photon of frequency
,
the electron makes a transition to the excited state. From there it
can decay back to the lower state by emitting a photon of frequency
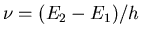 . There are 2 types of emission processes. In stimulated
emission, an incident photon of frequency
. There are 2 types of emission processes. In stimulated
emission, an incident photon of frequency 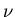 stimulates the
atom to make a transition from the higher state to the lower energy state
and emit another photon of frequency
stimulates the
atom to make a transition from the higher state to the lower energy state
and emit another photon of frequency 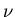 that is in phase with the first photon. The second photon is in phase because
the first photon causes the electron charge of the atom to oscillate
in phase with it and this oscillation causes the second photon to be
in phase with the first. So one photon comes in and two
photons leave. In spontaneous emission the excited atom spontaneously
decays to the lower energy state and emits a photon of frequency
that is in phase with the first photon. The second photon is in phase because
the first photon causes the electron charge of the atom to oscillate
in phase with it and this oscillation causes the second photon to be
in phase with the first. So one photon comes in and two
photons leave. In spontaneous emission the excited atom spontaneously
decays to the lower energy state and emits a photon of frequency
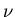 . One can regard this as emission stimulated by
zero point vacuum fluctuations of the electromagnetic field.
. One can regard this as emission stimulated by
zero point vacuum fluctuations of the electromagnetic field.
lec8emission.eps
Now suppose we start with an inverted population of atoms which are
each in their excited state. This can be accomplished by optically pumping
the atoms into their excited state with incident radiation. Now an
incident photon of frequency
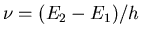 , which may have
been produced by spontaneous emission, stimulates one of the excited
atoms to emit a photon in phase with it. These two photons of frequency
, which may have
been produced by spontaneous emission, stimulates one of the excited
atoms to emit a photon in phase with it. These two photons of frequency
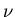 then produce stimulated emission from other excited atoms. If
we put the system in a cavity with reflecting walls at the ends, the
photons bounce back and forth, gaining more and more cohorts via
stimulated emission. If one of the walls is slightly transparent,
rather than being totally reflecting, part of this coherent monochromatic
beam escapes as a laser beam. Monochromatic means the photons are
all of one frequency
then produce stimulated emission from other excited atoms. If
we put the system in a cavity with reflecting walls at the ends, the
photons bounce back and forth, gaining more and more cohorts via
stimulated emission. If one of the walls is slightly transparent,
rather than being totally reflecting, part of this coherent monochromatic
beam escapes as a laser beam. Monochromatic means the photons are
all of one frequency 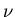 and coherent means that the photons are
all in phase. The fact that the photons are in phase means that
the amplitudes of the electromagnetic waves add constructively,
and this enhances the intensity and energy density concentration
of the beam. In fact a laser with less power than a typical light
bulb can burn a hole in a metal plate.
In contrast, white light is incoherent and nonmonochromatic
because there is no correlation in the times that the atoms make transitions.
and coherent means that the photons are
all in phase. The fact that the photons are in phase means that
the amplitudes of the electromagnetic waves add constructively,
and this enhances the intensity and energy density concentration
of the beam. In fact a laser with less power than a typical light
bulb can burn a hole in a metal plate.
In contrast, white light is incoherent and nonmonochromatic
because there is no correlation in the times that the atoms make transitions.
Let's make this more quantitative. Consider a set of two level systems
(atoms) in the presence of electromagnetic radiation. Let 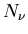 be the number of photons of frequency
be the number of photons of frequency 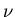 .
Let there be n1 atoms
in energy state E1 and n2 atoms in
energy state E2, where E2>E1 and
.
Let there be n1 atoms
in energy state E1 and n2 atoms in
energy state E2, where E2>E1 and
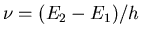 .
The rate of absorption of photons is proportional to the number of
photons of frequency
.
The rate of absorption of photons is proportional to the number of
photons of frequency 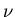 and to the concentration of atoms in state
1 which can absorb photons:
and to the concentration of atoms in state
1 which can absorb photons:
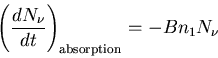 |
(1) |
where B is a constant of proportionality that depends on the properties
of states 1 and 2. The minus sign indicates that the photon density
decreases due to absorption by the atoms.
The rate of stimulated emission is proportional to the number
of photons of frequency 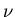 and to the concentration of atoms in state
2 which can be induced to emit photons of frequency
and to the concentration of atoms in state
2 which can be induced to emit photons of frequency 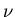 :
:
 |
(2) |
The plus sign indicates that emission increases the number of photons.
Spontaneous emission can occur even when there are no photons and
the corresponding rate is
 |
(3) |
So the total rate of change of the number of photons is the sum of
all these processes.
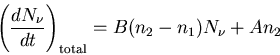 |
(4) |
This is an example of a rate equation. It tells us the rate of change
of a population due to emission and absorption. A and B are called
the Einstein coefficients.
Let us consider the steady state where the system is in equilibrium.
This is not the case for a laser, but let's look at it anyway.
In steady state the number of photons does not change with time,
so
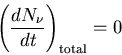 |
(5) |
or
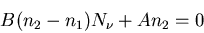 |
(6) |
Solving for 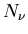 , we obtain
, we obtain
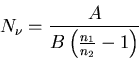 |
(7) |
In equilibrium the ratio of the populations of the excited and lower
states is given by the Boltzmann probability distribution
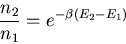 |
(8) |
or
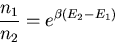 |
(9) |
Plugging this into (7) yields
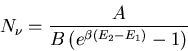 |
(10) |
On the other hand, we already know what the distribution is for photons
in equilibrium. It's just the Planck distribution that we derived when
we discussed black body radiation
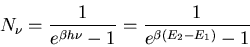 |
(11) |
Comparing (10) and (11) yields
Thus the coefficient in the spontaneous emission rate is exactly
the same as in the induced emission rate; the total emission rate is
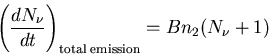 |
(13) |
Note that the form of the emission rate was deduced without knowing
the actual value of B; only detailed balancing arguments
were used. Detailed balancing is simply the idea that in equilibrium
the amount of energy absorbed and emitted must be equal.
Now let's consider the case of the laser. This is not an equilibrium
situation. The ratio of the emission and absorption of photons is given by
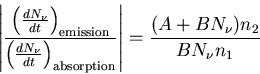 |
(14) |
In equilibrium
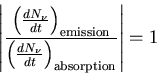 |
(15) |
but in a laser we have population inversion (n2>n1) and
 |
(16) |
So when the population is inverted, the rate of emission is
greater than the rate of absorption. This means that the applied
radiation of frequency
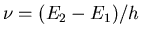 will be amplified in
intensity because of stimulated emission with much more radiation
emerging than entering. Of course, such a process will reduce
the population of the upper state until equilibrium is established.
In order to sustain the process, population inversion must be maintained.
One common way to do this is via optical pumping.
will be amplified in
intensity because of stimulated emission with much more radiation
emerging than entering. Of course, such a process will reduce
the population of the upper state until equilibrium is established.
In order to sustain the process, population inversion must be maintained.
One common way to do this is via optical pumping.
As an example let's consider a solid state laser that operates with a
ruby crystal in which some of the Al atoms in the Al2O3 molecules
are replaced by Cr atoms. These ``impurity'' chromium atoms account
for the laser action. The energy level scheme of chromium has 3 energy
levels
E1<E2<E3.
lec8ruby.eps
The energy difference E3-E1 corresponds
to a wavelength of about 5500 Å. Optical pumping occurs in
the following way. Pumping radiation with a wavelength 5500 Å is sent in and absorbed by Cr atoms which make a
transition from their ground state to the level with energy E3. This is
a short lived state (lifetime is about 10-8 seconds)
which decays spontaneously to the intermediate excited state
which is long lived (about
is sent in and absorbed by Cr atoms which make a
transition from their ground state to the level with energy E3. This is
a short lived state (lifetime is about 10-8 seconds)
which decays spontaneously to the intermediate excited state
which is long lived (about
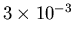 seconds). The net result
of the optical pumping is to invert the population such that n2>n1.
So when a Cr atom makes a transition from state 2 to state 1, it
emits a photon of wavelength 6943 Å
seconds). The net result
of the optical pumping is to invert the population such that n2>n1.
So when a Cr atom makes a transition from state 2 to state 1, it
emits a photon of wavelength 6943 Å which will stimulate transitions
in other Cr atoms. Because n2>n1, emission dominates over
absorption and an intensified coherent monochromatic beam results.
The ruby laser consists of a cylindrical rod with parallel, optically
flat reflecting ends, one of which is only partly reflecting. The
laser beam exits through this partially reflecting end. The emitted
photons that do not travel along the axis escape through the sides
before they are able to cause much stimlated emission. But those
photons that move exactly in the direction of the axis are reflected
several times, and they are capable of stimulating emission repeatedly.
Thus the number of photons is built up rapidly, those escaping from
the partially reflecting end giving a unidirectional beam of great
intensity and sharply defined wavelength.
which will stimulate transitions
in other Cr atoms. Because n2>n1, emission dominates over
absorption and an intensified coherent monochromatic beam results.
The ruby laser consists of a cylindrical rod with parallel, optically
flat reflecting ends, one of which is only partly reflecting. The
laser beam exits through this partially reflecting end. The emitted
photons that do not travel along the axis escape through the sides
before they are able to cause much stimlated emission. But those
photons that move exactly in the direction of the axis are reflected
several times, and they are capable of stimulating emission repeatedly.
Thus the number of photons is built up rapidly, those escaping from
the partially reflecting end giving a unidirectional beam of great
intensity and sharply defined wavelength.
There are many kinds of lasers-gas lasers, liquid lasers, semiconductor
lasers, and solid state lasers made from crystals.
These cover a wide range of the electromagnetic spectrum.
Lasers have a wide range of uses including medical physics, biophysics,
communications, and data storage (CD players). For example,
semiconductor lasers that are the size of a grain of sand are
used to send signals down optic fibers. I would like to spend a little
time describing some of the more amazing applications of lasers that
have been developed in recent years, namely laser trapping and laser
cooling.
Laser Trapping and Tweezers
Investigators have been able to use lasers to trap and manipulate atoms
and micron-size particles with astonishing control. For example,
laser tweezers use
a laser beam to hold and move organelles (like the mitochondria)
inside of living cells without puncturing the intervening membranes.
Steve Chu, who won the 1997 Nobel Prize in physics, has a cute video
showing a single DNA molecule attached to a polystyrene bead. By using
laser tweezers, they can whip the DNA molecule around at will. They
can also fix the ends of the DNA molecule and pluck it like a violin
string and study its modes of vibration.
Laser tweezers consist of a focussed laser beam. The particle is
trapped at the focal point where the field is most intense.
Laser tweezers work because of the ``dipole force'' on the trapped
particle. The oscillating
electric field 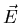 of the light induces a dipole moment
of the light induces a dipole moment 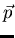 on the particle. If the induced dipole moment is in phase with
on the particle. If the induced dipole moment is in phase with
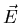 , the interaction energy
, the interaction energy
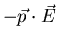 is lower in
high field regions. If the induced dipole moment is out of phase with
the driving field, the particle's energy is increased in the
electric field and the particle will feel a force ejecting it out of
the field. If we model the atom or particle as a damped harmonic
oscillator, the sign change of the dipole force is easy to understand.
is lower in
high field regions. If the induced dipole moment is out of phase with
the driving field, the particle's energy is increased in the
electric field and the particle will feel a force ejecting it out of
the field. If we model the atom or particle as a damped harmonic
oscillator, the sign change of the dipole force is easy to understand.
Recall that the electric susceptibility 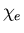 relates the polarization
relates the polarization
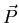 to the electric field
to the electric field 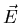 :
:
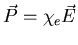 .
On a microscopic scale,
.
On a microscopic scale, 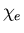 is related to the polarizability
is related to the polarizability 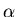 of an atom or molecule:
of an atom or molecule:
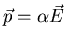 .
Let's consider an atom (or molecule) that's
in an oscillating electric field
.
Let's consider an atom (or molecule) that's
in an oscillating electric field
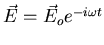 .
Since we're dealing with the macroscopic field
.
Since we're dealing with the macroscopic field 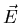 , we can
treat
, we can
treat 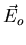 as a constant over the size of the atom. We're also
going to assume that
as a constant over the size of the atom. We're also
going to assume that 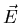 is small so that it causes only small
displacements of the electrons in the atom from their equilibrium
positions. This means that we can use the theory of small oscillations
to treat the electrons as harmonic oscillators. Finally we'll assume
that there is some damping force acting on the electrons that is
proportional to their velocity. Let x be the displacement parallel
to
is small so that it causes only small
displacements of the electrons in the atom from their equilibrium
positions. This means that we can use the theory of small oscillations
to treat the electrons as harmonic oscillators. Finally we'll assume
that there is some damping force acting on the electrons that is
proportional to their velocity. Let x be the displacement parallel
to 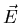 of an electron whose oscillator frequency is
of an electron whose oscillator frequency is 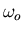 .
Then the equation of motion is
.
Then the equation of motion is
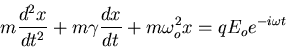 |
(17) |
This is the equation for a driven dampled harmonic oscillator. In the steady
state (after all transient behavior has stopped)
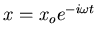 .
Plugging this in (17) yields
.
Plugging this in (17) yields
![\begin{displaymath}e^{-i\omega t}\left[-m\omega^2-im\gamma\omega+m\omega_o^2\right]x_o=qE_o
e^{-i\omega t}
\end{displaymath}](img34.gif) |
(18) |
Solving for xo, we obtain
![\begin{displaymath}x_o=\frac{qE_o}{m\left[\left(\omega_o^2-\omega^2\right)-i\gamma\omega\right]}
\end{displaymath}](img35.gif) |
(19) |
The dipole moment associated with the displacement of an electron is
p=qx where q is the electric charge. So the induced dipole moment is the
real part of
![\begin{displaymath}\vec{p}=\left[\frac{q^2}{m\left[\left(\omega_o^2-\omega^2\right)-
i\gamma\omega\right]}\right]\vec{E}
\end{displaymath}](img36.gif) |
(20) |
Comparing this with
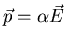 , we see that the polarizability
is
, we see that the polarizability
is
![\begin{displaymath}\alpha=\frac{q^2}{m\left[\left(\omega_o^2-\omega^2\right)-
i\gamma\omega\right]}
\end{displaymath}](img37.gif) |
(21) |
The real part is given by
![\begin{displaymath}\alpha_R=\frac{q^2\left(\omega_o^2-\omega^2\right)}
{m\left[\left(\omega_o^2-\omega^2\right)^2+(\gamma\omega)^2\right]}
\end{displaymath}](img38.gif) |
(22) |
Notice that below resonance (
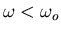 ),
), 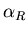 is positive
whereas above resonance
is positive
whereas above resonance 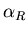 is negative.
is negative.
Going back to
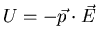 , we can use
, we can use
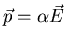 to write
to write
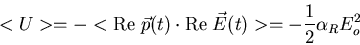 |
(23) |
where the average is over one period of the oscillating electric field.
The factor of 1/2 comes from this average (
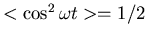 ).
``Re'' means take the real part of the complex number.
So the particle will be trapped at the
focal point of the laser beam (where E is largest) as long as the laser
is tuned below resonance. The particle will be pushed away if
the laser is tuned above resonance. One can use this repelling effect
to make a trampoline of light with atoms bouncing on it.
).
``Re'' means take the real part of the complex number.
So the particle will be trapped at the
focal point of the laser beam (where E is largest) as long as the laser
is tuned below resonance. The particle will be pushed away if
the laser is tuned above resonance. One can use this repelling effect
to make a trampoline of light with atoms bouncing on it.
Another way to understand how laser tweezers works is as a lensing effect.
A lens alters the distribution of momentum of light, and by Newton's
third law, the lens must experience a reaction force equal and opposite
to the rate of momentum change of the light. A small particle can act
as the lens.
tweezers.eps



Next: About this document ...
Clare Yu
1999-10-25
![]() , which may have
been produced by spontaneous emission, stimulates one of the excited
atoms to emit a photon in phase with it. These two photons of frequency
, which may have
been produced by spontaneous emission, stimulates one of the excited
atoms to emit a photon in phase with it. These two photons of frequency
![]() then produce stimulated emission from other excited atoms. If
we put the system in a cavity with reflecting walls at the ends, the
photons bounce back and forth, gaining more and more cohorts via
stimulated emission. If one of the walls is slightly transparent,
rather than being totally reflecting, part of this coherent monochromatic
beam escapes as a laser beam. Monochromatic means the photons are
all of one frequency
then produce stimulated emission from other excited atoms. If
we put the system in a cavity with reflecting walls at the ends, the
photons bounce back and forth, gaining more and more cohorts via
stimulated emission. If one of the walls is slightly transparent,
rather than being totally reflecting, part of this coherent monochromatic
beam escapes as a laser beam. Monochromatic means the photons are
all of one frequency ![]() and coherent means that the photons are
all in phase. The fact that the photons are in phase means that
the amplitudes of the electromagnetic waves add constructively,
and this enhances the intensity and energy density concentration
of the beam. In fact a laser with less power than a typical light
bulb can burn a hole in a metal plate.
In contrast, white light is incoherent and nonmonochromatic
because there is no correlation in the times that the atoms make transitions.
and coherent means that the photons are
all in phase. The fact that the photons are in phase means that
the amplitudes of the electromagnetic waves add constructively,
and this enhances the intensity and energy density concentration
of the beam. In fact a laser with less power than a typical light
bulb can burn a hole in a metal plate.
In contrast, white light is incoherent and nonmonochromatic
because there is no correlation in the times that the atoms make transitions.
![]() be the number of photons of frequency
be the number of photons of frequency ![]() .
Let there be n1 atoms
in energy state E1 and n2 atoms in
energy state E2, where E2>E1 and
.
Let there be n1 atoms
in energy state E1 and n2 atoms in
energy state E2, where E2>E1 and
![]() .
The rate of absorption of photons is proportional to the number of
photons of frequency
.
The rate of absorption of photons is proportional to the number of
photons of frequency ![]() and to the concentration of atoms in state
1 which can absorb photons:
and to the concentration of atoms in state
1 which can absorb photons:
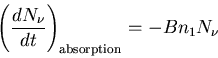


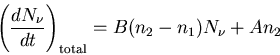
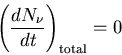
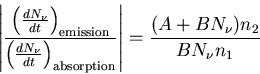
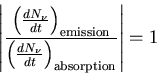

![]() is sent in and absorbed by Cr atoms which make a
transition from their ground state to the level with energy E3. This is
a short lived state (lifetime is about 10-8 seconds)
which decays spontaneously to the intermediate excited state
which is long lived (about
is sent in and absorbed by Cr atoms which make a
transition from their ground state to the level with energy E3. This is
a short lived state (lifetime is about 10-8 seconds)
which decays spontaneously to the intermediate excited state
which is long lived (about
![]() seconds). The net result
of the optical pumping is to invert the population such that n2>n1.
So when a Cr atom makes a transition from state 2 to state 1, it
emits a photon of wavelength 6943 Å
seconds). The net result
of the optical pumping is to invert the population such that n2>n1.
So when a Cr atom makes a transition from state 2 to state 1, it
emits a photon of wavelength 6943 Å![]() which will stimulate transitions
in other Cr atoms. Because n2>n1, emission dominates over
absorption and an intensified coherent monochromatic beam results.
The ruby laser consists of a cylindrical rod with parallel, optically
flat reflecting ends, one of which is only partly reflecting. The
laser beam exits through this partially reflecting end. The emitted
photons that do not travel along the axis escape through the sides
before they are able to cause much stimlated emission. But those
photons that move exactly in the direction of the axis are reflected
several times, and they are capable of stimulating emission repeatedly.
Thus the number of photons is built up rapidly, those escaping from
the partially reflecting end giving a unidirectional beam of great
intensity and sharply defined wavelength.
which will stimulate transitions
in other Cr atoms. Because n2>n1, emission dominates over
absorption and an intensified coherent monochromatic beam results.
The ruby laser consists of a cylindrical rod with parallel, optically
flat reflecting ends, one of which is only partly reflecting. The
laser beam exits through this partially reflecting end. The emitted
photons that do not travel along the axis escape through the sides
before they are able to cause much stimlated emission. But those
photons that move exactly in the direction of the axis are reflected
several times, and they are capable of stimulating emission repeatedly.
Thus the number of photons is built up rapidly, those escaping from
the partially reflecting end giving a unidirectional beam of great
intensity and sharply defined wavelength.
![]() of the light induces a dipole moment
of the light induces a dipole moment ![]() on the particle. If the induced dipole moment is in phase with
on the particle. If the induced dipole moment is in phase with
![]() , the interaction energy
, the interaction energy
![]() is lower in
high field regions. If the induced dipole moment is out of phase with
the driving field, the particle's energy is increased in the
electric field and the particle will feel a force ejecting it out of
the field. If we model the atom or particle as a damped harmonic
oscillator, the sign change of the dipole force is easy to understand.
is lower in
high field regions. If the induced dipole moment is out of phase with
the driving field, the particle's energy is increased in the
electric field and the particle will feel a force ejecting it out of
the field. If we model the atom or particle as a damped harmonic
oscillator, the sign change of the dipole force is easy to understand.
![]() relates the polarization
relates the polarization
![]() to the electric field
to the electric field ![]() :
:
![]() .
On a microscopic scale,
.
On a microscopic scale, ![]() is related to the polarizability
is related to the polarizability ![]() of an atom or molecule:
of an atom or molecule:
![]() .
Let's consider an atom (or molecule) that's
in an oscillating electric field
.
Let's consider an atom (or molecule) that's
in an oscillating electric field
![]() .
Since we're dealing with the macroscopic field
.
Since we're dealing with the macroscopic field ![]() , we can
treat
, we can
treat ![]() as a constant over the size of the atom. We're also
going to assume that
as a constant over the size of the atom. We're also
going to assume that ![]() is small so that it causes only small
displacements of the electrons in the atom from their equilibrium
positions. This means that we can use the theory of small oscillations
to treat the electrons as harmonic oscillators. Finally we'll assume
that there is some damping force acting on the electrons that is
proportional to their velocity. Let x be the displacement parallel
to
is small so that it causes only small
displacements of the electrons in the atom from their equilibrium
positions. This means that we can use the theory of small oscillations
to treat the electrons as harmonic oscillators. Finally we'll assume
that there is some damping force acting on the electrons that is
proportional to their velocity. Let x be the displacement parallel
to ![]() of an electron whose oscillator frequency is
of an electron whose oscillator frequency is ![]() .
Then the equation of motion is
.
Then the equation of motion is
![\begin{displaymath}x_o=\frac{qE_o}{m\left[\left(\omega_o^2-\omega^2\right)-i\gamma\omega\right]}
\end{displaymath}](img35.gif)
![\begin{displaymath}\vec{p}=\left[\frac{q^2}{m\left[\left(\omega_o^2-\omega^2\right)-
i\gamma\omega\right]}\right]\vec{E}
\end{displaymath}](img36.gif)
![\begin{displaymath}\alpha=\frac{q^2}{m\left[\left(\omega_o^2-\omega^2\right)-
i\gamma\omega\right]}
\end{displaymath}](img37.gif)
![\begin{displaymath}\alpha_R=\frac{q^2\left(\omega_o^2-\omega^2\right)}
{m\left[\left(\omega_o^2-\omega^2\right)^2+(\gamma\omega)^2\right]}
\end{displaymath}](img38.gif)
![]() , we can use
, we can use
![]() to write
to write