


Next: About this document ...
LECTURE 5
The One-Electron Atom
The problem with Bohr's theory is that it postulates an electron
whizzing around the nucleus with a velocity v and
centripetal acceleration v2/r. Classical electromagnetic
theory tells us that when a charged particle is accelerated, it
must radiate and lose energy. So Bohr's electron should be radiating
and losing energy which doesn't sound very stable. To treat the
electron properly, we need to use quantum mechanics. Let's start
by writing down Schrodinger's equation:
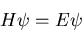 |
(1) |
(I'm going to drop the little hat on H. Just remember that it's
an operator.) Let's just consider a one electron atom so that we
don't have to worry about the interactions between electrons. The
Hamiltonian is
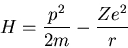 |
(2) |
where r is the distance from the nucleus, Z is the number of protons
(i.e., the atomic number), and m is the mass of the electron.
The first term is the kinetic energy of the electron and the second
term is the potential energy of the electron interacting
with the nucleus via the Coulomb interaction. Since p is an operator
(see lecture 1), we can write
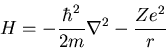 |
(3) |
It's always a good idea to look for symmetries before plunging into
a problem. So let's do that.
The potential produced by the nucleus is spherically symmetric. It is
called a central potential. The spherical symmetry means that we should
use spherical coordinates 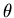 and
and 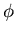 . Spherical symmetry
means that orbital angular momentum will be associated with
good quantum numbers
. Spherical symmetry
means that orbital angular momentum will be associated with
good quantum numbers 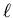 and m.
So we expect to be able to label the different
and m.
So we expect to be able to label the different 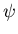 's with
's with 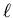 and
m. Here m is the z-component of
and
m. Here m is the z-component of 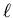 . It turns out that if
you write (3) in spherical coordinates, it is separable
into 3 differential equations: one for r, one for
. It turns out that if
you write (3) in spherical coordinates, it is separable
into 3 differential equations: one for r, one for 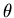 , and one
for
, and one
for 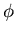 . Let R(r),
. Let R(r),
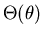 , and
, and
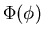 be the solutions of
these three equations. Then the total wavefunction can be written as a product:
be the solutions of
these three equations. Then the total wavefunction can be written as a product:
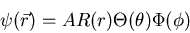 |
(4) |
where A is a constant.
We won't go through all the math needed to solve the Schrodinger equation.
Rather I'll just write down the answer. The energy eigenvalues are
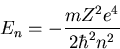 |
(5) |
Notice that the energy eigenvalues are quantized. n is called the
principal quantum number.
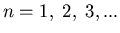 It is associated with the radial part of
the wavefunction. n can be thought of as labeling the atomic orbital
shells; the larger n is, the farther away the shell is from the nucleus.
The radius of a shell is roughly na where
a is very close to the Bohr radius in size. The radial part of the
wavefunction has an exponential factor:
It is associated with the radial part of
the wavefunction. n can be thought of as labeling the atomic orbital
shells; the larger n is, the farther away the shell is from the nucleus.
The radius of a shell is roughly na where
a is very close to the Bohr radius in size. The radial part of the
wavefunction has an exponential factor:
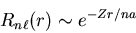 |
(6) |
Notice that
the exponential factor means that the probability that an electron
is located beyond a distance na falls off exponentially.
When Z=1 and n=1, eq. (5) reduces to -1 Rydberg:
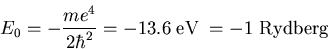 |
(7) |
This is a good energy to remember. It sets an upper bound for how
tightly electrons are bound to a nucleus.
The energy eigenfunctions are
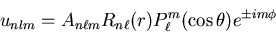 |
(8) |
The actual functions for various values of n, 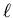 , and m are
given in Eisberg and Resnick on page 243.
Here we see that the orbital angular momentum quantum numbers are
associated with the angular part of the wavefunction. For a given
value of n, the values of
, and m are
given in Eisberg and Resnick on page 243.
Here we see that the orbital angular momentum quantum numbers are
associated with the angular part of the wavefunction. For a given
value of n, the values of 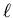 are
are
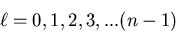 |
(9) |
By convention the 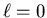 sublevel corresponds to an s orbital,
sublevel corresponds to an s orbital,
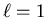 to a p orbital,
to a p orbital, 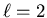 to a d orbital, and
to a d orbital, and 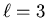 to an f orbital. These spectroscopic notations are the initial
letters of adjectives formerly used to describe spectral lines:
sharp, principal, diffuse, and fundamental. The spectral lines
were discovered before people realized where the lines came from.
For
to an f orbital. These spectroscopic notations are the initial
letters of adjectives formerly used to describe spectral lines:
sharp, principal, diffuse, and fundamental. The spectral lines
were discovered before people realized where the lines came from.
For 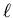 values
larger than 3, the letters used proceed alphabetically: g, h,
i, k, l, etc. (Note that j is omitted.)
For each value
of
values
larger than 3, the letters used proceed alphabetically: g, h,
i, k, l, etc. (Note that j is omitted.)
For each value
of 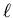 there are
there are
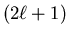 values of m:
values of m:
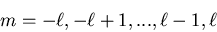 |
(10) |
Notice that
the energy eigenvalues (5) are independent of 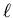 and m. This
means that for a given value of n, there n2 degenerate orbitals
which differ in their values of
and m. This
means that for a given value of n, there n2 degenerate orbitals
which differ in their values of 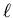 and m. Various effects which
we haven't included in the Hamiltonian can split this degeneracy.
For example, if the atom is in a magnetic field, the m levels are
split. This is known as the Zeeman effect and
m is known as the magnetic quantum number.
If we include the spin of the electron,
the maximum number of electrons that can reside
in a given energy level is 2n2.
and m. Various effects which
we haven't included in the Hamiltonian can split this degeneracy.
For example, if the atom is in a magnetic field, the m levels are
split. This is known as the Zeeman effect and
m is known as the magnetic quantum number.
If we include the spin of the electron,
the maximum number of electrons that can reside
in a given energy level is 2n2.
Let's look at the shapes of these various orbitals. The energy eigenfunctions
are orthogonal and this helps to determine the shapes they can have.
By orthogonal, I mean that they must satisfy
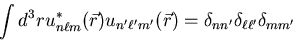 |
(11) |
where
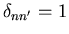 if
if
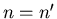 and
and
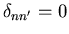 if
if
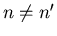 . (The fact that the eigenfunctions are normalized
to unity means that they are actually orthonormal.)
The n=1 level
has a single 1s orbital that is a spherically symmetric ball with no
nodes. (It's a nonzero constant at r=0.) The 2s orbital is also
spherically symmetric but it has a node at r=2a/Z due to orthogonality.
(A node is a place where the wavefunction is zero.) There are three
2p orbitals, and each has a nodal plane passing through the nucleus
at the origin. Each p orbital consists of two lobes that may be
considered to be oriented along the x, y, or z axis; hence, they
have the designations 2px, 2py, and 2pz. The 2pz orbital
corresponds to the n=2,
. (The fact that the eigenfunctions are normalized
to unity means that they are actually orthonormal.)
The n=1 level
has a single 1s orbital that is a spherically symmetric ball with no
nodes. (It's a nonzero constant at r=0.) The 2s orbital is also
spherically symmetric but it has a node at r=2a/Z due to orthogonality.
(A node is a place where the wavefunction is zero.) There are three
2p orbitals, and each has a nodal plane passing through the nucleus
at the origin. Each p orbital consists of two lobes that may be
considered to be oriented along the x, y, or z axis; hence, they
have the designations 2px, 2py, and 2pz. The 2pz orbital
corresponds to the n=2, 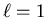 , m=0 orbital. The 2px and
2py orbitals correspond to symmetric and antisymmetric
linear combinations of the n=2,
, m=0 orbital. The 2px and
2py orbitals correspond to symmetric and antisymmetric
linear combinations of the n=2, 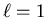 , m=1 and
n=2,
, m=1 and
n=2, 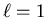 , m=-1 orbitals. For n=3, there is a 3s orbital,
three 3p orbitals, and five 3d orbitals (
3dx2-y2, 3dz2,
3dxy, 3dxz, and 3dyz). The shape of the 3dz2orbital is different from the others, but all these orbitals are energetically
equivalent.
, m=-1 orbitals. For n=3, there is a 3s orbital,
three 3p orbitals, and five 3d orbitals (
3dx2-y2, 3dz2,
3dxy, 3dxz, and 3dyz). The shape of the 3dz2orbital is different from the others, but all these orbitals are energetically
equivalent.
Each electronic state is labelled by 4 quantum numbers: n, 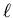 , m,
and sz. The Pauli exclusion principle prohibits 2 electrons from
having the same set of quantum numbers. If 2 electrons have the same
n,
, m,
and sz. The Pauli exclusion principle prohibits 2 electrons from
having the same set of quantum numbers. If 2 electrons have the same
n, 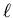 , m, then one is spin up and the other is spin down.
, m, then one is spin up and the other is spin down.
Spin-Orbit Coupling
Spin-orbit coupling refers to the coupling between the spin of an
electron in an atom and its orbital angular momentum. It arises from
relativistic effects and leads to a slight splitting of the degenerate energy
levels for a given value of n. There are 2 contributions to spin-orbit
coupling. The first comes from the fact that the spin of the electron
is associated with a magnetic moment 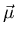 (see lecture 2) that
couples to any magnetic fields that might be present. As the electron
moves through the nuclear electric field, it sees both a magnetic and
an electric field. Special relativity says that an electric field in
a stationary reference frame looks like an electric and a magnetic
field in a moving frame.
(see lecture 2) that
couples to any magnetic fields that might be present. As the electron
moves through the nuclear electric field, it sees both a magnetic and
an electric field. Special relativity says that an electric field in
a stationary reference frame looks like an electric and a magnetic
field in a moving frame.
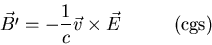 |
(12) |
This magnetic field couples to the electron's
magnetic moment and the magnetic moment precesses about the magnetic
field that it sees. This is Larmor precession.
This is one way that orbital motion couples to the
electron's spin.
The other way is called Thomas precession. It too is a relativistic
effect. Because of time dilation an observer at the nucleus and an
observer at rest on the electron would disagree about the amount of
time it takes for one particle to make a complete revolution about the
other. If the observer on the electron calls this time interval T,
then an observer on the nucleus will find it to be
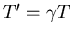 ,
where
,
where
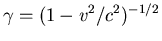 and v is the speed of the electron
about the nucleus.
Now, in the rest frame of the electron, the spin vector maintains
its direction in space, so that to the observer on the nucleus, this
spin vector appears to precess at a rate equal to the difference between the
two angular velocities
and v is the speed of the electron
about the nucleus.
Now, in the rest frame of the electron, the spin vector maintains
its direction in space, so that to the observer on the nucleus, this
spin vector appears to precess at a rate equal to the difference between the
two angular velocities 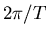 and
and
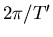 . The Thomas precession
frequency turns out to be half that of the Larmor precession frequency and
of the opposite sign.
. The Thomas precession
frequency turns out to be half that of the Larmor precession frequency and
of the opposite sign.
Both of these effects couple the electron spin to its orbital motion.
Putting these two effects together leads to a spin-orbit coupling term
in the Hamiltonian:
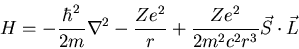 |
(13) |
where
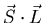 is an operator with units of angular momentum
squared (
is an operator with units of angular momentum
squared (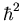 ). This extra term in the Hamiltonian splits the
degenerate energy level for a given value of n into several degenerate
levels. The splittings are of order 1 part in 104.
(
). This extra term in the Hamiltonian splits the
degenerate energy level for a given value of n into several degenerate
levels. The splittings are of order 1 part in 104.
(
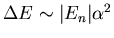 , where the fine structure constant
, where the fine structure constant
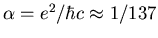 . So
. So
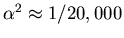 .)
These small splittings lead to fine structure in the spectral
lines.
.)
These small splittings lead to fine structure in the spectral
lines.
Because spin and orbital angular momentum are coupled together
Lz and Sz are not conserved, though L2 and
S2 are conserved. (
[S2,H]=[L2,H]=0 but
![$[S_z,H]\neq 0$](img40.gif) and
and
![$[L_z, H]\neq 0$](img41.gif) ).
So
).
So 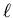 and s are good quantum numbers,
but
and s are good quantum numbers,
but 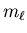 and ms are not.
But the total angular momentum
and ms are not.
But the total angular momentum
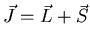 is conserved and therefore, j and mJ are good quantum numbers.
(see lecture 2)
is conserved and therefore, j and mJ are good quantum numbers.
(see lecture 2)
Many Electron Atom
Other sources of energy level splitting
There are several other sources of electron level splitting. For example,
there is also another small relatistic correction to the energy due
to the fact that in special relativity, the energy
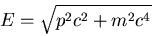 |
(14) |
This shifts the energy levels by the same order of magnitude as
spin-orbit coupling.
When there are many electrons, dipole-dipole (spin-spin) interactions
between the electrons as well as the electrostatic
Coulomb interactions between
them lead to energy splittings.
Russell-Saunders or LS Coupling
The relative strengths of these
effects varies depending on what kind of atom we
have. In some cases spin-orbit effects are quite small compared
to spin-spin and electrostatic interactions between the electrons.
In this case LS or Russell-Saunders coupling is a good place to start.
In this coupling it is assumed that the individual orbital angular
momenta 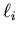 are quite strongly coupled together, as are
the individual spin angular momenta si. So
are quite strongly coupled together, as are
the individual spin angular momenta si. So 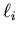 and
si are not good quantum numbers. (Here
and
si are not good quantum numbers. (Here 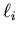 is the orbital
angular momentum of the ith electron and si is the spin
angular momentum of the ith electron.) However,
the total orbital angular momentum
is the orbital
angular momentum of the ith electron and si is the spin
angular momentum of the ith electron.) However,
the total orbital angular momentum
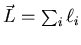 of all the electrons and the total
spin angular momentum
of all the electrons and the total
spin angular momentum
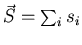 of all the electrons are
close to being good quantum numbers. The resultant
of all the electrons are
close to being good quantum numbers. The resultant 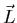 and
and 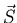 are less strongly coupled to each other and their resultant is
are less strongly coupled to each other and their resultant is 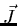 .
.
Hund's Rule
Atomic levels may have the same electron configuration (e.g., 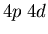 )
but different total L and S. Hund's rule is an empirical principle
concerning the relative position of levels with the same configuration
but different L and S: The term with the greatest possible
value of S (for the given electron configuration) and the greatest
possible value of L (for this S) has the lowest energy. In other words,
Hund's rule states that electrons are distributed among the orbitals
of a subshell in a way that gives the maximum number of unpaired electrons
with parallel spins, and the maximum value of the orbital angular momentum
L consistent with this S. The value of the total angular momentum
J is equal to |L-S| when the shell is less than half full and
to L+S when the shell is more than half full. When the shell is
exactly half full, the maximization of the S gives L=0, so that
J=S.
)
but different total L and S. Hund's rule is an empirical principle
concerning the relative position of levels with the same configuration
but different L and S: The term with the greatest possible
value of S (for the given electron configuration) and the greatest
possible value of L (for this S) has the lowest energy. In other words,
Hund's rule states that electrons are distributed among the orbitals
of a subshell in a way that gives the maximum number of unpaired electrons
with parallel spins, and the maximum value of the orbital angular momentum
L consistent with this S. The value of the total angular momentum
J is equal to |L-S| when the shell is less than half full and
to L+S when the shell is more than half full. When the shell is
exactly half full, the maximization of the S gives L=0, so that
J=S.
For example, suppose there are four equivalent d electrons outside
the closed shells in an atom. The magnetic quantum number of each d
electron can take five values: 0, 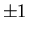 ,
, 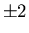 . Hence all four
electrons can have the same spin component ms=1/2, and the
maximum possible total spin is S=2. Now we must assign the maximum
value of
. Hence all four
electrons can have the same spin component ms=1/2, and the
maximum possible total spin is S=2. Now we must assign the maximum
value of
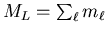 , namely
, namely
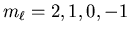 . This
implies that ML=2. Thus the maximum value of L for S=2is also 2. The shell is less than half full (there can be up to 10
d electrons), so J=|L-S|=0.
. This
implies that ML=2. Thus the maximum value of L for S=2is also 2. The shell is less than half full (there can be up to 10
d electrons), so J=|L-S|=0.
Another example would be nitrogen which has 3 electrons in
the 2p orbitals. The electronic configuration is
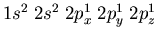 . Notice that the electrons
distribute themselves among the p orbitals rather than bunching
up in, say,
. Notice that the electrons
distribute themselves among the p orbitals rather than bunching
up in, say,
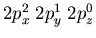 . The standard way to
write the electronic configuration of nitrogen is
. The standard way to
write the electronic configuration of nitrogen is
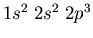 where it is understood that the electrons will
spread out among the orbitals.
where it is understood that the electrons will
spread out among the orbitals.
To understand why S should be as large as possible, let us suppose
that the total wavefunction 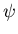 for the electrons can be
written as the product
of a spin wavefunction
for the electrons can be
written as the product
of a spin wavefunction 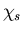 and a space wavefunction
and a space wavefunction 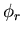 .
.
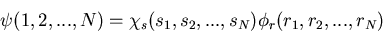 |
(15) |
where si is the spin coordinate of the ith electron and ri is
the spatial coordinate of the ith electron.
Since electrons are fermions, 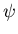 must be antisymmetric under
the interchange of any 2 particles.
must be antisymmetric under
the interchange of any 2 particles.
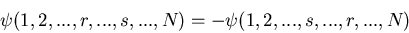 |
(16) |
We can satisfy this by having 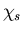 symmetric and
symmetric and 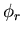 antisymmetric or vice-versa. For example, if we have 2 electrons, they
can be in a singlet (S=0) or a triplet (S=1) state. The triplet state
has a symmetric spin wavefunction and an antisymmetric spatial wavefunction.
antisymmetric or vice-versa. For example, if we have 2 electrons, they
can be in a singlet (S=0) or a triplet (S=1) state. The triplet state
has a symmetric spin wavefunction and an antisymmetric spatial wavefunction.
and
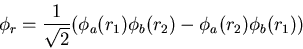 |
(17) |
The singlet state has an antisymmetric spin wavefunction and a
symmetric spatial wavefunction.
![\begin{displaymath}\chi_{S=0,m_s=0}=\frac{1}{\sqrt{2}}[\uparrow\downarrow-\downarrow\uparrow]
\end{displaymath}](img65.gif) |
(18) |
and
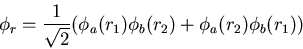 |
(19) |
The nodes in the antisymmetric
spatial wavefunction of the triplet helps to keep the electrons apart and
reduce the Coulomb repulsion much more than the symmetric spatial
wavefunction of the singlet. This tends to be true in general since
larger spin tends to be associated with more nodes in the spatial
wavefunction.
Spectroscopic Notation
The energy eigenstates of almost all atoms can be described in terms
of a quantum number L which defines the net orbital angular momentum
of all the electrons, a quantum number S which defines the
net spin angular momentum of all of the electrons, and a quantum number
J which defines the total angular momentum
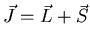 .
L is always an integer, and S is integral or half-integral
depending upon whether the total number of electrons in the atom is even
or odd. In this general case the multiplicity of the level is equal
to 2S+1 or 2L+1, whichever is smaller.
.
L is always an integer, and S is integral or half-integral
depending upon whether the total number of electrons in the atom is even
or odd. In this general case the multiplicity of the level is equal
to 2S+1 or 2L+1, whichever is smaller.
Spectroscopic notation for labeling the energy eigenstates
has the following form:
Since it is most often the case that S is smaller than L, so that
the multiplicity is equal to 2S+1, the preceding superscript has come
to be always associated with S. This index is always equal to 2S+1,
and is equal to the true multiplicity of the level only if S is less than,
or equal to, L. The value of the total angular momentum J for a
given level is indicated by the subscript.
The numerical values of L are correlated with the
letter notation according to the table:
L 0 1 2 3 4 5 6 7 8 9 10
-----------------------------------------------------------------
Letter S P D F G H I K L M N
For an example consider the 4 equivalent d electrons that we
showed had L=S=2 and J=0. The spectroscopic notation for this
is state is 5D0.
Another example is shown in the figure
lec5level.eps



Next: About this document ...
Clare Yu
1999-10-11
![]() , m,
and sz. The Pauli exclusion principle prohibits 2 electrons from
having the same set of quantum numbers. If 2 electrons have the same
n,
, m,
and sz. The Pauli exclusion principle prohibits 2 electrons from
having the same set of quantum numbers. If 2 electrons have the same
n, ![]() , m, then one is spin up and the other is spin down.
, m, then one is spin up and the other is spin down.
![]() ,
where
,
where
![]() and v is the speed of the electron
about the nucleus.
Now, in the rest frame of the electron, the spin vector maintains
its direction in space, so that to the observer on the nucleus, this
spin vector appears to precess at a rate equal to the difference between the
two angular velocities
and v is the speed of the electron
about the nucleus.
Now, in the rest frame of the electron, the spin vector maintains
its direction in space, so that to the observer on the nucleus, this
spin vector appears to precess at a rate equal to the difference between the
two angular velocities ![]() and
and
![]() . The Thomas precession
frequency turns out to be half that of the Larmor precession frequency and
of the opposite sign.
. The Thomas precession
frequency turns out to be half that of the Larmor precession frequency and
of the opposite sign.
![]() and
and
![]() ).
So
).
So ![]() and s are good quantum numbers,
but
and s are good quantum numbers,
but ![]() and ms are not.
But the total angular momentum
and ms are not.
But the total angular momentum
![]() is conserved and therefore, j and mJ are good quantum numbers.
(see lecture 2)
is conserved and therefore, j and mJ are good quantum numbers.
(see lecture 2)
![]() ,
, ![]() . Hence all four
electrons can have the same spin component ms=1/2, and the
maximum possible total spin is S=2. Now we must assign the maximum
value of
. Hence all four
electrons can have the same spin component ms=1/2, and the
maximum possible total spin is S=2. Now we must assign the maximum
value of
![]() , namely
, namely
![]() . This
implies that ML=2. Thus the maximum value of L for S=2is also 2. The shell is less than half full (there can be up to 10
d electrons), so J=|L-S|=0.
. This
implies that ML=2. Thus the maximum value of L for S=2is also 2. The shell is less than half full (there can be up to 10
d electrons), so J=|L-S|=0.
![]() . Notice that the electrons
distribute themselves among the p orbitals rather than bunching
up in, say,
. Notice that the electrons
distribute themselves among the p orbitals rather than bunching
up in, say,
![]() . The standard way to
write the electronic configuration of nitrogen is
. The standard way to
write the electronic configuration of nitrogen is
![]() where it is understood that the electrons will
spread out among the orbitals.
where it is understood that the electrons will
spread out among the orbitals.
![]() for the electrons can be
written as the product
of a spin wavefunction
for the electrons can be
written as the product
of a spin wavefunction ![]() and a space wavefunction
and a space wavefunction ![]() .
.
![\begin{eqnarray*}\chi_{S=1,m_s=1}&=&\uparrow\uparrow\\
\chi_{S=1,m_s=0}&=&\frac...
...narrow\uparrow]\\
\chi_{S=1,m_s=-1}&=&\\ downarrow\downarrow\\
\end{eqnarray*}](img63.gif)