


Next: About this document ...
LECTURE 4
Reversible and Irreversible Processes
Consider an isolated system in equilibrium (i.e., all microstates are
equally probable), with some number of microstates 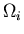 that are
accessible to the system. Suppose some internal constraint
is removed but the total energy and particle number remain constant.
Now the system can be in any of the
that are
accessible to the system. Suppose some internal constraint
is removed but the total energy and particle number remain constant.
Now the system can be in any of the 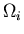 microstates plus
whatever new microstates become available when the constraint is removed.
The total number of accessible microstates after the constraint is removed
is
microstates plus
whatever new microstates become available when the constraint is removed.
The total number of accessible microstates after the constraint is removed
is 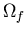 .
.
Note that the system is not in equilibrium immediately
after removing the constraint. Only a fraction of the states
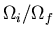 are occupied. By the H theorem, the system now
evolves in time (approaches equilibrium) in such a manner as to
make more equal the probability of the system being found in any of the
are occupied. By the H theorem, the system now
evolves in time (approaches equilibrium) in such a manner as to
make more equal the probability of the system being found in any of the
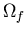 microstates. (If some constraint on an isolated system
is removed, the parameters readjust in such a way that
microstates. (If some constraint on an isolated system
is removed, the parameters readjust in such a way that
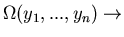 maximum.)
maximum.)
Note also that if
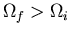 , then after final equilibrium
is achieved, simply restoring the initial constraint may not restore the
system to its initial condition. In such a case we talk about an
irreversible process.
, then after final equilibrium
is achieved, simply restoring the initial constraint may not restore the
system to its initial condition. In such a case we talk about an
irreversible process.
As an example, consider a box divided into two parts by a partition.
=3.0 true in
ONboxes.eps
Removing the partition increases the number of microstates accessible
to the system as the volume accessible to each molecule increases. After
the new equilibrium is reached, simply restoring the partition will
not return the system to its original condition.
To summarize, if some constraint (or constraints) is removed in an
isolated system in equilibrium, then the number of microstates accessible
to the system can either remain constant or increase, i.e.,
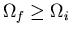 . If
. If
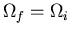 , then the process
is reversible. If
, then the process
is reversible. If
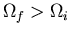 , the process is irreversible.
, the process is irreversible.
Dependence of Density of States on External Parameters
We have already shown that the equilibrium condition for two thermally
interacting systems is that the 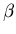 parameters of both systems be equal.
We now want to determine the equilibrium conditions for two systems that
interact thermally and mechanically. We will need, and therefore must
derive, the relationship
parameters of both systems be equal.
We now want to determine the equilibrium conditions for two systems that
interact thermally and mechanically. We will need, and therefore must
derive, the relationship
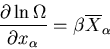 |
(1) |
where
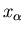 is an external parameter and the generalized force is
is an external parameter and the generalized force is
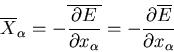 |
(2) |
In other words, we want to know how the number of states 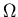 changes
when work is done on the system, i.e., when the external parameters
are changed. When the external parameters are changed, the energy levels
shift. For example, consider standing waves or resonant modes in
a cavity. If we change the size of the cavity, the wavelength of the
standing waves changes, and the associated energy levels change.
(Quantum mechanically, the frequency and energy go as
changes
when work is done on the system, i.e., when the external parameters
are changed. When the external parameters are changed, the energy levels
shift. For example, consider standing waves or resonant modes in
a cavity. If we change the size of the cavity, the wavelength of the
standing waves changes, and the associated energy levels change.
(Quantum mechanically, the frequency and energy go as  where
where 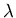 is the wavelength.) This is why a piccolo has a higher
pitch than a flute or a tuba.
is the wavelength.) This is why a piccolo has a higher
pitch than a flute or a tuba.
Consider 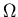 as a function of E and x. (Let's drop the
subscript
as a function of E and x. (Let's drop the
subscript 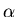 for a moment and concentrate on one external
parameter.) Then how does
for a moment and concentrate on one external
parameter.) Then how does
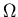 depend on x? When x is changed by an amount dx, the energy
Er(x) of each microstate is changed by an amount
depend on x? When x is changed by an amount dx, the energy
Er(x) of each microstate is changed by an amount
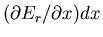 . Let
. Let
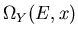 be the number
of states which have an energy between E and
be the number
of states which have an energy between E and
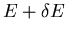 when the external
parameter is x and which are such that
the derivative
when the external
parameter is x and which are such that
the derivative
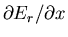 is between Y and
is between Y and
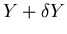 .
The total number of states is
.
The total number of states is
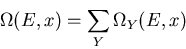 |
(3) |
Consider a particular energy E. When the external parameter is changed, some
states which originally had an energy less than E will acquire an
energy greater than E and vice-versa. Those states
for which
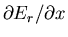 has the particular value
Y change their energy by Ydx. Hence all those states located within an
energy Ydx below E will change their energy from a value smaller than
E to one greater than E.
has the particular value
Y change their energy by Ydx. Hence all those states located within an
energy Ydx below E will change their energy from a value smaller than
E to one greater than E.
=3.0 true in
energyrange.eps
The number
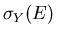 of such states is
thus given by the number per unit energy multiplied by the energy range
Ydx, i.e., by
of such states is
thus given by the number per unit energy multiplied by the energy range
Ydx, i.e., by
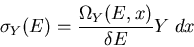 |
(4) |
Different states have their energy changed by different amounts Ydx.
Hence the total number of states 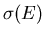 whose energy is changed
from a value less than to a value greater than E is given by summing
over all possible values of Y:
whose energy is changed
from a value less than to a value greater than E is given by summing
over all possible values of Y:
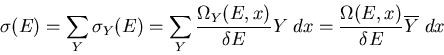 |
(5) |
where the mean value of Y is
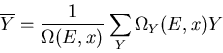 |
(6) |
Note that
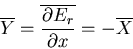 |
(7) |
where X is the generalized force conjugate to the external parameter x.
Let us now consider the total number of states
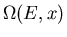 between
E and
between
E and
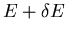 . When the parameter x changes from x to x+dx,
the number of states changes by
. When the parameter x changes from x to x+dx,
the number of states changes by
![$[\partial\Omega(E,x)/\partial x]dx$](img29.gif) which must be due to [the number of states which enter this range from below
by having their energy changed from a value less than E to one greater
than E] minus [the number of states that leave through the top by having
their energy changed from a value less than
which must be due to [the number of states which enter this range from below
by having their energy changed from a value less than E to one greater
than E] minus [the number of states that leave through the top by having
their energy changed from a value less than
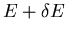 to one greater
than
to one greater
than
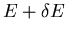 ]:
]:
=3.0 true in
moveout.eps
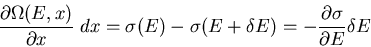 |
(8) |
Using (5), this becomes
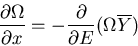 |
(9) |
or
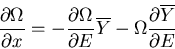 |
(10) |
Dividing both sides by 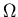 , we have
, we have
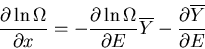 |
(11) |
The second term on the right is negligible since
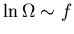 where
the number of degrees of freedom f is on the order of 1023.
So we can write
where
the number of degrees of freedom f is on the order of 1023.
So we can write
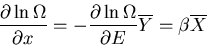 |
(12) |
since
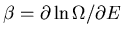 . If we have several external
parameters, we can easily generalize this to the desired relation:
. If we have several external
parameters, we can easily generalize this to the desired relation:
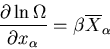 |
(13) |
From (12) and the definition of the entropy
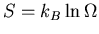 ,
we can write
,
we can write
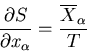 |
(14) |
Equilibrium Conditions
Consider now two systems A and A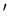 in contact
which can exchange heat and do work on each other.
A is described by the macroscopic parameters E and x, while A
in contact
which can exchange heat and do work on each other.
A is described by the macroscopic parameters E and x, while A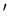 is
described by
is
described by
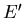 and
and
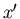 where
where
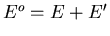 and
and
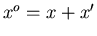 . Then
. Then
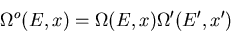 |
(15) |
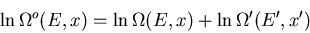 |
(16) |
At equilibrium
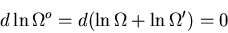 |
(17) |
But
and
since
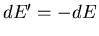 and
and
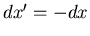 . The equilibrium condition
. The equilibrium condition
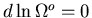 implies
implies
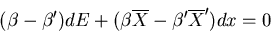 |
(20) |
Both coefficients must vanish since E and x are independent variables.
Hence the equilibrium conditions are
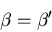 |
(21) |
and
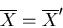 |
(22) |
where
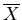 is any generalized force. So if
is any generalized force. So if
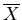 is the
pressure p, then the pressures and temperatures are equal in
equilibrium.
is the
pressure p, then the pressures and temperatures are equal in
equilibrium.
Quasi-Static Processes
Almost by definition, when a system undergoes a process and changes,
it cannot be exactly described by equilibrium statistical mechanics
or thermodynamics. However we can talk about a quasi-static process
in which the system progresses slowly enough to be arbitrarily close
to equilibrium throughout the process. We can think of the system
progressing through a series of equilibrium states infinitesimally
separated from each other.
Consider first an infinitesimal quasi-static process in which a system
A is brought from an equilibrium state described by mean energy E and
external parameter
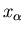 to an infinitesimally different equilibrium
state described by E+dE and
to an infinitesimally different equilibrium
state described by E+dE and
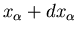 due to an interaction
with system A
due to an interaction
with system A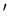 . Since
. Since
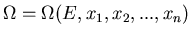 , we can write
, we can write
Let the total mechanical work done by the system be
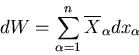 |
(24) |
Hence
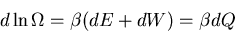 |
(25) |
since
This statement is valid for any quasistatic process, even if work of any form
is done by the system. But
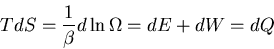 |
(27) |
or
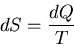 |
(28) |
This statement is true for any infinitesimal quasi-static processes, even
if work is done.
Note that if dQ=0, then dS=0. Thus entropy does not
change in an infinitesimal, adiabatic process. An adiabatic process is one in
which there is no heat transfer.
We can extend this discussion to a finite process which proceeds
quasi-statically through
a series of equilibrium states, and obtain the result that if the external
parameters of a thermally isolated system are changed
quasi-statically by a finite amount, then
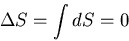 |
(29) |
In other words, the entropy is unchanged.
Since
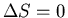 , the number of accessible states is unchanged. This
means that the process is reversible.
However, it is worth emphasizing that even if a system is thermally
isolated so that it absorbs no heat, its entropy will increase
if processes take place which are not quasi-static.
, the number of accessible states is unchanged. This
means that the process is reversible.
However, it is worth emphasizing that even if a system is thermally
isolated so that it absorbs no heat, its entropy will increase
if processes take place which are not quasi-static.
Note that while dQ is an inexact differential, dQ/T is an exact
differential, i.e.,
 |
(30) |
provided the path of integration is a series of equilibrium states. Only
for equilibrium states is the entropy a defined concept. Entropy
(
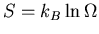 ) just depends on the equilibrium state of the system and not
on how it got there. So the entropy difference is path independent.
The inverse
temperature (1/T) is thus an integrating factor for dQ. This, in fact,
is another way mathematically to define the concept of temperature. The
reciprocal temperature can be defined as the integrating factor of dQ.
) just depends on the equilibrium state of the system and not
on how it got there. So the entropy difference is path independent.
The inverse
temperature (1/T) is thus an integrating factor for dQ. This, in fact,
is another way mathematically to define the concept of temperature. The
reciprocal temperature can be defined as the integrating factor of dQ.
Limiting Behavior of Entropy
In quantum mechanics,
as the energy of a system decreases, it goes towards its ground state.
The lowest possible energy state of a system is called its ground state.
Let's call the ground state energy Eo. Corresponding to this energy
there is usually only one possible microstate of the system. Or there
may be a relatively small number of such states, all with the same energy
Eo; in this case the ground state is then said to be
``degenerate.'' If there is just one state with energy Eo, the
ground state is nondegenerate. Then
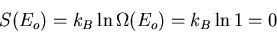 |
(31) |
Even if the ground state is degenerate,
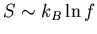 which is
negligibly small compared to the entropy at large energy. Since
which is
negligibly small compared to the entropy at large energy. Since
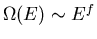 at large energies,
at large energies,
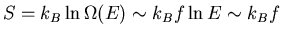 which is much larger than S at low energies.
In general at low energies S is vanishingly small and we can write
which is much larger than S at low energies.
In general at low energies S is vanishingly small and we can write
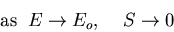 |
(32) |
We can state this in terms of the temperature. Recall that we can
think of the temperature roughly as the energy per degree of freedom.
As the temperature drops, the energy of the system drops. If we plot
the 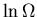 versus E, it looks something like:
versus E, it looks something like:
=3.0 true in
lnOmega.eps
The slope gives the inverse temperature
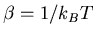 :
:
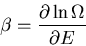 |
(33) |
Notice that the slope gets steeper as
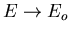 . So
. So
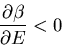 |
(34) |
or
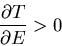 |
(35) |
At Eo the slope is vertical,
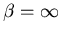 , and T=0.
So as the temperature approaches zero, the system approaches its
ground state, the energy approaches Eo and the entropy approaches
zero.
, and T=0.
So as the temperature approaches zero, the system approaches its
ground state, the energy approaches Eo and the entropy approaches
zero.
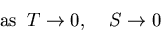 |
(36) |
In applying this, one must be sure that equilibrium arguments apply
to the system in question. Equation (36) is the third
law of thermodynamics.
Ideal Gas
It is about time we applied a few of these ideas to a simple system. Perhaps
the simplest nontrivial example of a large collection of particles is
the ideal gas. We will come back to this example several times because
of its simplicity. An ideal gas consists of a collection of noninteracting
particles treated as mass points. The only energy available is the kinetic
energy of the particles; no internal excitations, no internal vibrations, no
rotation and no interactions.
We will first treat the ideal gas as a simple classical system.
Consider N particles with mass m and momentum 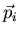 . The
particles are identical. The total energy is
. The
particles are identical. The total energy is
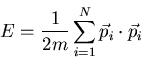 |
(37) |
In classical statistical mechanics, the total number of microstates is the
total volume of the accessible phase space divided by the volume of a unit
cell of phase space. N particles require 3N spatial coordinates and
3N components of momenta to specify a point in the 6N dimensional
phase space. The number of microstates is
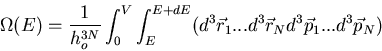 |
(38) |
Now the coordinates and momenta are independent. Also each integration over
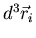 yields a factor of V, the volume of the container in which
the gas is contained. We obtain
yields a factor of V, the volume of the container in which
the gas is contained. We obtain
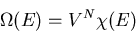 |
(39) |
where
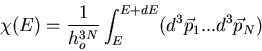 |
(40) |
Thus
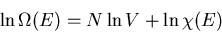 |
(41) |
The generalized force corresponding to the external parameter V is the
pressure p. Thus
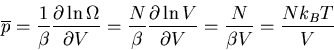 |
(42) |
or
where n=N/V is the number of molecules per unit volume. Alternatively
one can write 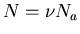 where
where 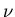 is the number of moles of gas present
and Na is Avogadro's number. Then (43) becomes
is the number of moles of gas present
and Na is Avogadro's number. Then (43) becomes
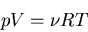 |
(44) |
where R=NakB is called the ``gas constant.''
This equation is known as an equation of state. It relates the macroscopic
parameters pressure, volume, and temperature. We will talk more about
equations of state in our discussion of thermodynamics. In general
equations of state relate p, V, and T. 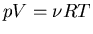 is the equation
of state for an ideal gas and it is the most famous one.
is the equation
of state for an ideal gas and it is the most famous one.
The parameter 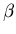 is given by
is given by
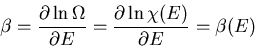 |
(45) |
The temperature of an ideal gas is a function only of the total energy
and does not depend on V. We can invert this to say that the mean energy is
solely a function of the temperature
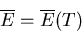 |
(46) |
For an ideal gas the mean energy
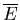 does not depend on the volume.
Changing the volume of the container changes the mean distance between
the particles and affects the strength of their mutual interaction. But in
the case of an ideal gas, there are no interactions. Since the kinetic
energies do not depend on the distances between particles, the mean energy
is unaffected by the change in volume.
Later we will find the complete relation between
does not depend on the volume.
Changing the volume of the container changes the mean distance between
the particles and affects the strength of their mutual interaction. But in
the case of an ideal gas, there are no interactions. Since the kinetic
energies do not depend on the distances between particles, the mean energy
is unaffected by the change in volume.
Later we will find the complete relation between
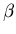 and E, and find that
and E, and find that
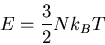 |
(47) |
The van der Waals gas
Just to show you that there is more than one equation of state, I would
like to mention the van der Waals gas. The molecules in
real gases interact with one another and one approximation to a real gas
is known as a van der Waals gas. The equation of state for a van der Waals
gas is
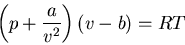 |
(48) |
where 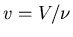 is the molar volume. a and b are constants. This is
an empirical equation known as the van der Waals equation. van der Waals
interactions refer to spontaneous electronic charge fluctuations on a molecule
which produces a short lived dipole moment. These fluctuations induce
complementary fluctuations on neighboring molecules and the molecules attract
one another. So the molecules are a little closer together than
noninteracting molecules, i.e., the gas is compressed a little bit; the
term a/v2 represents this additional positive pressure. On the other hand
there are also short-range repulsive forces between the molecules which
keep them apart sufficiently to prevent them from occupying the same place
at the same time. The term b represents the volume occupied by the
molecules themselves and which must thus be subtracted from the volume
available to any one molecule in the container. Notice that for
a=b=0 or in the limit of a very dilute gas (
is the molar volume. a and b are constants. This is
an empirical equation known as the van der Waals equation. van der Waals
interactions refer to spontaneous electronic charge fluctuations on a molecule
which produces a short lived dipole moment. These fluctuations induce
complementary fluctuations on neighboring molecules and the molecules attract
one another. So the molecules are a little closer together than
noninteracting molecules, i.e., the gas is compressed a little bit; the
term a/v2 represents this additional positive pressure. On the other hand
there are also short-range repulsive forces between the molecules which
keep them apart sufficiently to prevent them from occupying the same place
at the same time. The term b represents the volume occupied by the
molecules themselves and which must thus be subtracted from the volume
available to any one molecule in the container. Notice that for
a=b=0 or in the limit of a very dilute gas (
 ),
(48) reduces to the equation of state for an ideal gas.
),
(48) reduces to the equation of state for an ideal gas.



Next: About this document ...
Clare Yu
2002-04-16
![]() that are
accessible to the system. Suppose some internal constraint
is removed but the total energy and particle number remain constant.
Now the system can be in any of the
that are
accessible to the system. Suppose some internal constraint
is removed but the total energy and particle number remain constant.
Now the system can be in any of the ![]() microstates plus
whatever new microstates become available when the constraint is removed.
The total number of accessible microstates after the constraint is removed
is
microstates plus
whatever new microstates become available when the constraint is removed.
The total number of accessible microstates after the constraint is removed
is ![]() .
.
![]() are occupied. By the H theorem, the system now
evolves in time (approaches equilibrium) in such a manner as to
make more equal the probability of the system being found in any of the
are occupied. By the H theorem, the system now
evolves in time (approaches equilibrium) in such a manner as to
make more equal the probability of the system being found in any of the
![]() microstates. (If some constraint on an isolated system
is removed, the parameters readjust in such a way that
microstates. (If some constraint on an isolated system
is removed, the parameters readjust in such a way that
![]() maximum.)
maximum.)
![]() , then after final equilibrium
is achieved, simply restoring the initial constraint may not restore the
system to its initial condition. In such a case we talk about an
irreversible process.
, then after final equilibrium
is achieved, simply restoring the initial constraint may not restore the
system to its initial condition. In such a case we talk about an
irreversible process.
![]() . If
. If
![]() , then the process
is reversible. If
, then the process
is reversible. If
![]() , the process is irreversible.
, the process is irreversible.
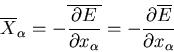
![]() as a function of E and x. (Let's drop the
subscript
as a function of E and x. (Let's drop the
subscript ![]() for a moment and concentrate on one external
parameter.) Then how does
for a moment and concentrate on one external
parameter.) Then how does
![]() depend on x? When x is changed by an amount dx, the energy
Er(x) of each microstate is changed by an amount
depend on x? When x is changed by an amount dx, the energy
Er(x) of each microstate is changed by an amount
![]() . Let
. Let
![]() be the number
of states which have an energy between E and
be the number
of states which have an energy between E and
![]() when the external
parameter is x and which are such that
the derivative
when the external
parameter is x and which are such that
the derivative
![]() is between Y and
is between Y and
![]() .
The total number of states is
.
The total number of states is
![]() has the particular value
Y change their energy by Ydx. Hence all those states located within an
energy Ydx below E will change their energy from a value smaller than
E to one greater than E.
has the particular value
Y change their energy by Ydx. Hence all those states located within an
energy Ydx below E will change their energy from a value smaller than
E to one greater than E.
![]() of such states is
thus given by the number per unit energy multiplied by the energy range
Ydx, i.e., by
of such states is
thus given by the number per unit energy multiplied by the energy range
Ydx, i.e., by
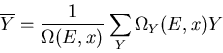
![]() between
E and
between
E and
![]() . When the parameter x changes from x to x+dx,
the number of states changes by
. When the parameter x changes from x to x+dx,
the number of states changes by
![]() which must be due to [the number of states which enter this range from below
by having their energy changed from a value less than E to one greater
than E] minus [the number of states that leave through the top by having
their energy changed from a value less than
which must be due to [the number of states which enter this range from below
by having their energy changed from a value less than E to one greater
than E] minus [the number of states that leave through the top by having
their energy changed from a value less than
![]() to one greater
than
to one greater
than
![]() ]:
]:
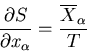
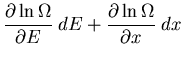
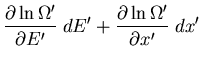
![]() to an infinitesimally different equilibrium
state described by E+dE and
to an infinitesimally different equilibrium
state described by E+dE and
![]() due to an interaction
with system A
due to an interaction
with system A![]() . Since
. Since
![]() , we can write
, we can write
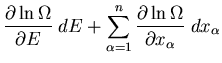
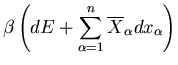
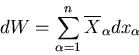
![]() . The
particles are identical. The total energy is
. The
particles are identical. The total energy is
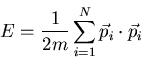
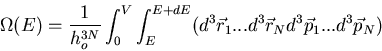
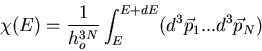
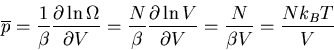
![]() is given by
is given by