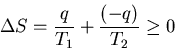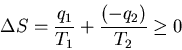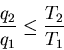Next: About this document ...
LECTURE 8
Heat Engines
Heat engines have important technological importance. The basic idea
is that one would like to extract heat from a heat reservoir, where
that energy is spread randomly over a huge number of degrees of freedom,
and convert it into work. By work we mean energy associated with a single
degree of freedom connected with an external parameter of some outside
device. Typically the engine goes through a cycle, returning to its initial
state after having turned some heat into work. Think about the gasoline
engine in your car. Ideally we would like a perfect engine that converts
all the heat into useable work:
=2.0 true in
perfectEngine.eps
This obeys the first law of thermodynamics but it violates the second
law. (Nothing's perfect.) From our previous discussions we know that
work can be converted into heat in an irreversible process in which
the distribution of systems over accessible states becomes more random
so that entropy increases. One cannot expect to simply reverse the process
and convert internal energy randomly distributed over all its degrees of
freedom into work that changes one macroscopic degree of freedom. It's
possible but fantastically improbable. It amounts to decreasing the
number of accessible states, i.e., to decreasing the entropy. The second
law of thermodynamics requires that the total entropy of the complete
system (consisting of the heat engine, the outside device on which it
does work, and the heat reservoir) be such that in a cycle
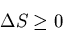 |
(2) |
Now the heat engine itself returns to its previous state after a cycle is
complete so its entropy is unchanged. The outside
device on which work is done by changing an external parameter has no
entropy change because we envision that it has an external parameter that
changes without doing it at the expense of its other degrees of freedom.
For example consider lifting a weight by extracting heat from a heat
reservoir. So dQ<0. But
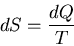 |
(3) |
This implies that dS<0 and that violates the second law of thermodynamics.
In fact one way of stating the second law is to say
- It is impossible to construct a perfect heat engine.
(This statement is sometimes called Kelvin's formulation of the second
law of thermodynamics.) We can make realizable heat engines that do not
violate the second law by bringing in a second heat bath to absorb some heat.
Since it absorbs heat, its entropy is increased. If it increases its entropy
enough, it will ensure that the entire system has a net increase in entropy.
Let's suppose that we have 2 reservoirs, a hotter one at temperature T1from which heat is extracted and a cooler one at temperature T2 which
absorbs some heat. In between a heat engine absorbs some heat q1 from
the hotter reservoir, does some work and dumps some heat q2 into the cooler
reservoir.
=2.0 true in
realEngine.eps
In this case the first law requires that in a cycle
After one cycle the engine and the device on which work is done are
back where they started, so their entropy does not change. The net increase
in entropy must come from the heat reservoirs:
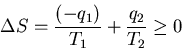 |
(5) |
From (4) q2=q1-w. Plugging this into (5), we get
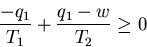 |
(6) |
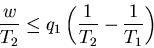 |
(7) |
The equals sign holds for quasi-static processes. We can rewrite this last
equation as
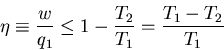 |
(8) |
where
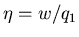 is called the ``efficiency'' of the engine. For a
perfect engine
is called the ``efficiency'' of the engine. For a
perfect engine
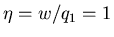 . For a real engine
. For a real engine 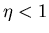 :
:
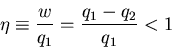 |
(9) |
since some heat does not get transformed into work but is dumped into
another heat reservoir. The most efficient engine occurs for quasi-static
processes where
 . From (8) this maximum efficiency is
. From (8) this maximum efficiency is
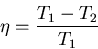 |
(10) |
Furthermore any engine which operates between these two reservoirs
in a quasi-static manner has this same maximum efficiency.
Carnot Engine
Conceptually the simplest engine operating quasi-statically between
2 heat reservoirs is called a ``Carnot engine.'' Let x denote the
external parameter of the engine M; changes in this parameter give
rise to the work performed by the engine. Let the engine initially
be in a state where x=xa and its temperature T=T2, the temperature
of the colder heat reservoir. The Carnot engine then goes through a cycle
consisting of 4 steps, all performed quasi-statically. Let's label the
macrostates of the engine by small letters a, b, c, and d.
=3.0 true in
pV.eps
=3.0 true in
TS.eps
- 1.
-
 :
The engine is thermally insulated. Its external
parameter is changed slowly until the engine temperature reaches T1.
Thus
:
The engine is thermally insulated. Its external
parameter is changed slowly until the engine temperature reaches T1.
Thus
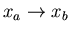 such that
such that
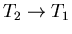 .
.
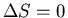 since the system is thermally isolated and the process is quasi-static.
(One can think of a piston compressing gas in a thermally insulated cylinder.)
since the system is thermally isolated and the process is quasi-static.
(One can think of a piston compressing gas in a thermally insulated cylinder.)
- 2.
-
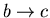 :
The engine is now placed in thermal contact with the
heat reservoir at temperature T1. Its external parameter is changed
further, the engine remaining at temperature T1 and absorbing some heat
q1 from the reservoir. Thus
:
The engine is now placed in thermal contact with the
heat reservoir at temperature T1. Its external parameter is changed
further, the engine remaining at temperature T1 and absorbing some heat
q1 from the reservoir. Thus
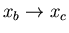 such that q1 is
absorbed by the engine. (The gas in the cylinder is allowed to expand
while its temperature is maintained at T1. It absorbs heat q1.)
such that q1 is
absorbed by the engine. (The gas in the cylinder is allowed to expand
while its temperature is maintained at T1. It absorbs heat q1.)
- 3.
-
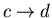 :
The engine is again thermally insulated. Its
external parameter is changed in such a direction that its temperature
goes back to T2. Thus
:
The engine is again thermally insulated. Its
external parameter is changed in such a direction that its temperature
goes back to T2. Thus
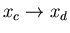 such that
such that
 .
.
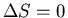 .
(The gas in the thermally insulated
cylinder is allowed to expand until the gas temperature is T2.)
.
(The gas in the thermally insulated
cylinder is allowed to expand until the gas temperature is T2.)
- 4.
-
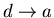 :
The engine is now placed in thermal contact with
the heat reservoir at temperature T2. Its external parameter is then
changed until it returns to its initial value xa, the engine remaining
at temperature T2 and dumping some heat q2 into this reservoir.
Thus
:
The engine is now placed in thermal contact with
the heat reservoir at temperature T2. Its external parameter is then
changed until it returns to its initial value xa, the engine remaining
at temperature T2 and dumping some heat q2 into this reservoir.
Thus
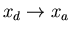 and heat q2 is given off by the engine.
(The gas is compressed while its temperature is maintained at T2.
It puts heat q2 into the reservoir.)
and heat q2 is given off by the engine.
(The gas is compressed while its temperature is maintained at T2.
It puts heat q2 into the reservoir.)
The engine is now back in its initial state and the cycle is completed.
The amount of work done during a Carnot cycle is given by
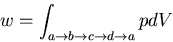 |
(11) |
This corresponds to the shaded area in the pV plot. Usually the
cooler reservoir is just the air. Think of your car engine giving off
heat to the radiator that in turn gives the heat to the air.
We are used to gasoline powered engines in our car, steam engines,
nuclear powered generators, etc. One type of engine you may not be
aware of is a solid state engine with no moving parts. If you take
a bar of a metal or a semiconductor, heat one end and cool the other,
you can get electrons to flow from the hot end to the cold end and
these electrons do work.
=2.5 true in
seebeck.eps
Solid state engines are used in deep space probes where moving parts
would wear out after a few years. The heat source can be a radioactive
substance like plutonium.
Refrigerators
A refrigerator is a device which removes heat from a cooler reservoir and
puts it in a hotter reservoir. A perfect refrigerator would do this
heat transfer without affecting the environment in any other way, i.e.,
no work would need to be done.
=1.5 true in
perfectFrig.eps
But a perfect refrigerator would violate
the second law. The total entropy has to increase:
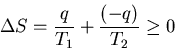 |
(12) |
or
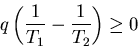 |
(13) |
which is impossible since q>0 and T1>T2. Thus we can state the
second law of thermodynamics as:
- It is impossible to make a perfect refrigerator.
This is known as the Clausius formulation of the second law.
We are all familiar with this. We have to plug in our refrigerators in
the kitchen. In fact about 95% of your electric bill is due to the electricity
gobbled up by your refrigerator. A real refrigerator requires that some
work w be done to make it run. If it takes heat q2 from the cooler
reservoir at temperature T2 and transfers heat q1 to the hotter
reservoir at temperature T1, then the first law requires that
=2.5 true in
realFrig.eps
So the heat absorbed from the colder reservoir is less than the heat given
off to the hotter reservoir. The second law requires that
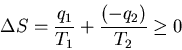 |
(15) |
or
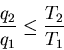 |
(16) |
where the equals sign holds only for a refrigerator operating between
two reservoirs quasi-statically. One way to make a such a refrigerator
would be to run the Carnot engine in reverse.



Next: About this document ...
Clare Yu
2002-04-29