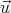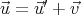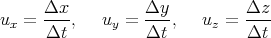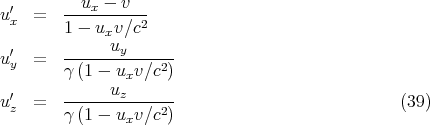Physics 51A: Modern Physics
Prof. Clare Yu
email: cyu@uci.edu
phone: 949-824-6216
Office: 210E RH
Winter 2013
CHAPTER 1
Introduction
Have you ever watched a horror or science fiction movie where everything starts out very
normal and ordinary, but then strange and bizarre things begin to happen? Well, special
relativity is like that. Let me give you a brief preview.
We live in a 3 dimensional world: length, width, height. Actually, it’s 4 dimensional if you
include time. For example, if you have a meeting to go to, you need to know where and when it
will be, i.e., you need to specify the position (location) and the time. We tend to think of
spatial dimensions as very different from time. Positions are fixed in time and space but
time passes. However, as we shall see, Einstein’s theory of special relativity tells us
that space can transform into time and time can be transformed into space. Weird,
huh? Space and time are not as ordinary as they appear to be. This turns out to
be a consequence of the fact that the speed of light is the universal speed limit;
nothing (technically speaking, no information) can travel faster than the speed of
light.
Static Reference Frames
But let’s start out with the boring and ordinary. (Pay attention because things will slowly
start to get weird and you won’t even realize it at first.) In particular, let’s talk about frames of
reference. If we specify a position 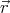 = (x,y,z), we are measuring (x,y,z) with respect to a
given frame of reference. That same position could have different coordinates in another
reference frame. For example, consider the point P in Figure 1. In one frame of reference P has
the coordinates (x = 3,y = 4) while in the other (primed) reference frame, P has the
coordinates (x′ = 1,y′ = 1). The position of P is measured relative to a coordinate
system.
= (x,y,z), we are measuring (x,y,z) with respect to a
given frame of reference. That same position could have different coordinates in another
reference frame. For example, consider the point P in Figure 1. In one frame of reference P has
the coordinates (x = 3,y = 4) while in the other (primed) reference frame, P has the
coordinates (x′ = 1,y′ = 1). The position of P is measured relative to a coordinate
system.
Similarly, when we measure the time of an event, it is with respect to when t = 0. For
example, when we say that the year is 2013, we are measuring with respect to the year 0 A.D.
Of course, the laws of physics hold and are the same (invariant) no matter where the origin of
the coordinates or the time t = 0 is set.
Moving Reference Frames
Now let’s consider 2 reference frames moving relative to one another with a constant
velocity 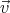 . Each reference frame has an observer. For example, suppose reference frame S is
fixed to the ground and reference frame S’ is fixed to a train moving along the tracks with
constant velocity
. Each reference frame has an observer. For example, suppose reference frame S is
fixed to the ground and reference frame S’ is fixed to a train moving along the tracks with
constant velocity 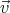 . Each observer is standing still but thinks the other observer is moving. The
person on the train tracks sees the train and the passenger moving at velocity
. Each observer is standing still but thinks the other observer is moving. The
person on the train tracks sees the train and the passenger moving at velocity 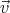 . The
passenger on the train sees the person standing on the tracks go by with velocity
-
. The
passenger on the train sees the person standing on the tracks go by with velocity
-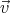 .
.
If the passenger is standing and drops a ball straight down, then the ball will fall at his feet.
The observer on the tracks sees the ball follow a parabola and land to the right of where it was
released. This is because the ball is traveling horizontally with the same speed as the train.
(See Figure 1.2 in the book.)
If the passenger throws the ball at a velocity 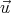 ′ relative to the train, then the observer
standing on the ground sees the ball traveling at a velocity
′ relative to the train, then the observer
standing on the ground sees the ball traveling at a velocity 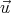 given by the sum of the train
velocity and the velocity of the ball with respect to the train:
given by the sum of the train
velocity and the velocity of the ball with respect to the train:
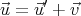 | (1) |
The book calls this equation the classical velocity-addition formula. As we shall see, this
doesn’t hold in Einstein’s Theory of Special Relativity.
The next question is “Do Newton’s Laws of Motion hold in moving reference frames?” As
your book describes in Section 1.3, Newton’s 3 Laws of Motion hold in all reference frames that
are moving at constant velocity (including v = 0) with respect to one another, i.e., in
unaccelerated reference frames. These reference frames are often called inertial frames. Let’s
review what these laws of motion are:
- The law of inertia: A body on which no external forces act moves with constant
velocity.
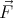 = m
= m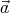
- For every action, there is an equal and opposite reaction.
So Newton’s laws of motion are invariant in all inertial frames of reference.
The speed of light is c in all inertial frames.
What about the laws of electromagnetism, i.e., Maxwell’s equations? Are they
invariant in inertial frames of reference? Classically, the answer is no, but Einstein
showed that the right answer is yes. To see this, let’s consider the speed of light
c.
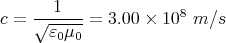 | (2) |
where ε0 and μ0 are the permittivity and the permeability of the vacuum. These constants
appear in Maxwell’s equations. So if Maxwell’s equations hold in a frame S, then light travels
the same speed c in all directions.
Now suppose a pulse of light is moving along the +x axis in frame S at speed c. Consider
another frame of reference S′ moving along the x axis with velocity 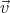 . According to
Eq. (1), an observer in S′ would measure the speed of the light pulse to be c - v.
Similarly, if a pulse of light were traveling at speed c in S in the -x direction, then the
observer in S′ would measure the speed of the light coming toward him to be c + v. For
light traveling at some oblique angle with respect to the x-axis, the observer in S′
would measure the speed of light to be between c - v and c + v. Since Maxwell’s
equations demand that the speed of light be exactly c as given by Eq. (2), we conclude
that the laws of electromagnetism, unlike those of mechanics, are not valid in frame
S′.
. According to
Eq. (1), an observer in S′ would measure the speed of the light pulse to be c - v.
Similarly, if a pulse of light were traveling at speed c in S in the -x direction, then the
observer in S′ would measure the speed of the light coming toward him to be c + v. For
light traveling at some oblique angle with respect to the x-axis, the observer in S′
would measure the speed of light to be between c - v and c + v. Since Maxwell’s
equations demand that the speed of light be exactly c as given by Eq. (2), we conclude
that the laws of electromagnetism, unlike those of mechanics, are not valid in frame
S′.
This is what people believed before Einstein came along. They believed that light
propagated through a medium called ether which filled the vacuum, and that there was just
one frame, the ether frame, in which light traveled at speed c. In any frame moving with
respect to the ether, like earth, light would be measured as traveling at some other
velocity.
The obvious thing to do is to measure the speed of light experimentally. But that’s hard
to do because light goes so fast. If you turn on a flashlight and then ask someone
with a stopwatch to see how long it takes for the light to travel across the room,
that would be impossible since the light travels so fast. However, between 1880 and
1887, Albert Michelson, later assisted by Edward Morley, measured the speed of
light. Some of those experiments were done near here, and that may be why we
have a road called Michelson. They figured that the speed of the earth with respect
to the ether was probably comparable to the earth’s speed as it circled the sun,
i.e.,
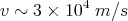 | (3) |
This is about 1/10,000 the speed of light. So they expected to see the speed of light differ from
its value in the vacuum by about 1 part in 104. To do such a sensitive measurement, they built
an interferometer that split a beam of light into 2 beams that traveled perpendicular to each
other, and then later were deflected to intersect at one point. If the beams traveled at different
velocities or different distances, this could be detected by constructive or destructive
interference of the light waves. Surprisingly, they found that light traveled at the speed c in all
directions. Later and more precise experiments have found the same result. Light travels at the
same speed in all directions in all inertial reference frames. (More details about the
Michelson-Morley experiment can be found in your book in section 1.5.) This means
that the laws of electromagnetism are the same (invariant) in all inertial frames of
reference.
This means that the classical velocity-addition formula (Eq. (1)) doesn’t hold for light. In
other words, if an observer on the ground shines light along the +x-axis, the observer in
the moving train measures the speed of the light as c, irrespective of the train’s
velocity. Now things are starting to get weird. Einstein was the first to work out
the consequences of this startling finding, and the result was the Theory of Special
Relativity.
Postulates of Relativity
First let us expand our definition of an inertial frame to be any reference frame (that is,
system of coordinates x, y, z, and time t) where all the laws of physics hold in their
simplest form. (Your book adds the stipulation “simplest form” to exclude things like
introducing a “fictitious” centrifugal force so that the laws of statics hold in an rotating
frame.)
Now here are the postulates of relativity:
- If S is an inertial frame and if a second frame S′ moves with a constant velocity
relative to S, then S′ is also an inertial frame. This means that there is no absolute
motion, and that everything is relative, so to speak. Going back to the train and
the observers, the train is moving relative to the observer standing next to the train
tracks, and the ground is moving relative to the observer on the train. No inertial
frame is better than any other frame.
- In all inertial frames, light travels through the vacuum with the same speed, c =
299, 792, 458 m/s in any direction. This is the conclusion of the Michelson-Morley
experiment.
Measurement of Time
It
turns out that the time between 2 events can be different in different inertial frames, so we
need to be very careful about how time is measured. Basically we can think of a reference
frame S filled with a team of observers, each with a clock and all the clocks are
synchronized to the same time. They can synchronize their clocks by sending a flash
of light at a specified time and take into account the time it takes for the light to
travel between clocks. Any event that happens in frame S will be noted by a nearby
observer and she can tell the other observers when the event happened according to her
clock.
The Relativity of Time: Time Dilation
It turns out that the time between 2 events is different when viewed from two different
frames that are moving at a constant velocity relative to one another. So let’s consider 2
inertial frames of reference: one anchored to the ground that we’ll call S, and the other in a
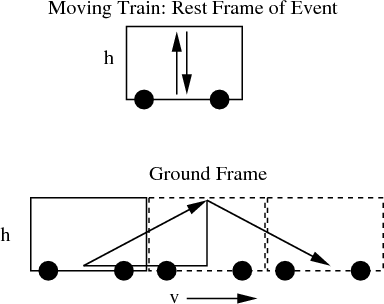
train moving at velocity 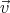 relative to the ground. We’ll call the train frame S′. In the train, a
flash of light leaves the floor, travels up to the ceiling where it hits a mirror, and is reflected
back to the floor. When it returns to the floor, a beep is heard by the passenger on the train.
The height of the railcar is h, so the time for the light to make a round trip up to the ceiling
and back is
relative to the ground. We’ll call the train frame S′. In the train, a
flash of light leaves the floor, travels up to the ceiling where it hits a mirror, and is reflected
back to the floor. When it returns to the floor, a beep is heard by the passenger on the train.
The height of the railcar is h, so the time for the light to make a round trip up to the ceiling
and back is
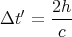 | (4) |
This is the time interval recorded by a passenger in the train, i.e., in the frame S′. (See
Figure 2.) The light flash leaves and returns to the same place on the floor of the
train.
In the ground frame let us denote the time interval by Δt. The ground observer would say
that the flash leaves at one place and returns to another because the train moved in the
interval. (See Figure 2.) We can apply Pythagoras’ theorem to calculate the distance
cΔt∕2 from the flash on the floor to the ceiling as observed by the person on the
ground:
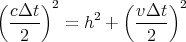 | (5) |
Solving for Δt gives
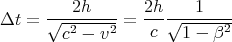 | (6) |
where
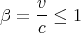 | (7) |
We will see β a lot, so it’s good to be familiar with it. Another variable that is used a lot is γ
defined as
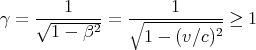 | (8) |
So we can write
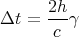 | (9) |
Using Eq. (4), we obtain
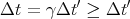 | (10) |
It turns out that this equation applies to the interval between any 2 events that
occur at the same place in the frame S′. Let’s look at this equation. Since γ ≥ 1,
it says that the ground observer measures a longer time interval between 2 events
than the train based observer. Basically time runs slower on the train. Notice, as a
check, that if v = 0 (the train is standing still), then Δt = Δt′ which is what we
expect.
The faster the train goes, i.e., the bigger v is, the slower time is on the train. If the train
goes at the speed of light, then
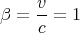 | (11) |
and
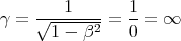 | (12) |
The time interval measured on the ground would be infinity which is absurd. What if v > c?
Then β = v∕c > 1, and γ would be imaginary, which is unphysical (impossible). The speed of
light c is the speed limit of the universe. Nothing can go faster than the speed of light.
(Technically, no information can go faster than the speed of light.) We shall see that nothing
with nonzero mass can travel at the speed of light. Anything with mass must travel at a speed
less than the speed of light. So β < 1 and γ ≥ 1.
What if v = 0.99c? Then β = 0.99, and
The frame of reference where 2 events (in our case the flash and the beep) occur at the
same place is special. The time measured between the 2 events that occur in the
same place is called the proper time. It is designated by Δt0 with a subscript zero
to indicate the events occurred at the same place in this reference frame. This is
always the shortest time measured between these 2 events in any reference frame. The
time measured in any frame between these two events is always greater or equal to
Δt0:
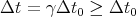 | (14) |
This effect is called time dilation.
We have seen that time goes slower in moving frames of reference. How much slower does it
go on a jet plane traveling at 500 miles/hour? Say you fly across the country on a 5-hour flight.
How much slower does time go for you compared to a friend on the ground? Use the
fact that c = 186, 000 miles/sec and that there are 3600 seconds in an hour to find
β = 500∕(3600 × 1.85 × 105) = 7.47 × 10-7, γ = 1 + (β2∕2) = 1 + 2.79 × 10-13. So the difference
is (2.79 × 10-13) × (5 hours) × (3600 seconds/hour)= 5.02 × 10-9 ≈ 5 ns which is
imperceptible.
Experimental Evidence for Time Dilation
There is good experimental evidence confirming time dilation and the conclusion that time
goes slower in moving reference frames. For example, in 1971, jet planes carried atomic clocks
around the world, and then the clocks were compared to atomic ground based clocks. The
predicted difference was 275 ± 21 ns, and the measured discrepancy was 273 ± 7 ns which is in
good agreement.
Another confirmation is provided everyday by unstable subatomic particles which
disintegrate. When they decay is random, but the half-life t1∕2 is well known. The half-life is
the time it takes for half of a large sample of particles to decay. For example, the charged π
meson, or pion, is formed by collisions between rapidly moving atomic nuclei in particle
accelerators. Its half-life is
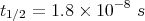 | (15) |
At Fermilab near Chicago, pions are produced moving very close to the speed of
light:
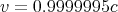 | (16) |
and they must travel about 1 km to the experimental area. Now if we didn’t know about
relativity, how long (in lab time) would it take for them to get there?
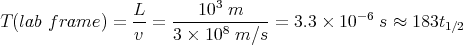 | (17) |
which implies that there won’t be any pions left by time they get 1 km.
But let’s see what relativity says. Note that
So So
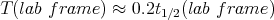 | (20) |
So in the lab, the pion’s half-life increases by a factor of γ because the pions are moving so fast.
The actual time of flight in the lab is only about 1/5 the relevant half-life. So plenty of pions
make it to the experimental area.
Length Contraction
We have seen that time depends on the reference frame. It turns out that length or distance
does too. We can still use distance = velocity × time since this is just the definition of
velocity.
We again consider 2 reference frames: one (S′) on a train moving with constant velocity 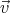 and the other (S) fixed to the ground. We want to measure the length of the train. An observer
on the ground measures the time t1 when the front of the train passes him, and the time t2
that the back of the train passes him. Then he calculates the length ℓ of the train to
be
and the other (S) fixed to the ground. We want to measure the length of the train. An observer
on the ground measures the time t1 when the front of the train passes him, and the time t2
that the back of the train passes him. Then he calculates the length ℓ of the train to
be
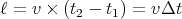 | (21) |
What do observers on the train measure to be the length ℓ′ of the train? Let’s put one observer
at the front of the train and one at the back of the train. When the observer at the front passes
a tree on the ground, he records the time t1′. When the observer at the back of the train passes
that same tree, he records the time t2′. So the observers on the train calculate the length of the
train to be
 | (22) |
Δt′ and Δt are different so ℓ′ and ℓ must be different. We need to relate Δt′ and Δt using the
time dilation formula. In this case the front of the train opposite the tree and the back of the
train opposite the same tree occur at the same place on the ground. So the time on the ground
is the proper time. Thus, we have
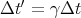 | (23) |
Plugging this into Eq. (22) yields
or
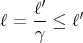 | (25) |
So the observers on the train and on the ground measure a different length for the train,
unless the train is standing still. The observers on the ground measure a shorter
train than the passengers on the train do. The faster the train, the shorter the train
according to the people on the ground. If the train were moving at the speed of
light, γ = ∞, and the people on the ground would say the length of the train is zero
which is absurd. Again, nothing with mass can travel at or faster than the speed of
light.
When we measure length or distance in the rest frame of the object, we call that length the
proper length ℓ0. The length of the train in the rest frame of the train is ℓ0 = ℓ′, and we can
write
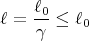 | (26) |
The maximum length of an object is in its rest frame. All other frames of reference measure
ℓ ≤ ℓ0. This is called length contraction or Lorentz contraction. Basically, the faster
an object moves, the shorter it appears to be in the direction of motion. Weird,
huh?
Evidence for Length Contraction
Length contraction is well established experimentally. Let’s go back to the pion experiment
where we saw that in the lab, the pions’ half-life was increased by a factor of γ. Suppose,
however, that we go to the pions’ rest frame where the pions are stationary and there is no
increase in their half-life. How do they reach the experimental area? From the point of view of
the pions, the pipe or tunnel is moving, and the length of the pipe is contracted by a factor of
γ. So if the length of the pipe is L = 1 km in the lab, the pions measure it to be
L∕γ = L∕1000 = 1 meter. Of course, the number of pions surviving the journey is the same in
both reference frames.
Lengths Perpendicular to the Direction of Motion
It turns out that lengths perpendicular to the direction of motion are not changed. (see
page 25 in your book for more details) Only lengths parallel to the direction of motion
experience Lorentz contraction.
Lorentz Transformation
Let
us now consider a more general problem. If we know the coordinates x, y, z, and the time t of
an event measured in a frame S, what are the coordinates x′, y′, z′, and t′ of the same event in
the frame S′?
Let us start by setting up the two frames of reference: S anchored to the ground and S′
anchored to a train moving with velocity 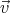 relative to the ground. We choose the x-axis and
the x′-axis to lie along the same line, parallel to
relative to the ground. We choose the x-axis and
the x′-axis to lie along the same line, parallel to 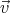 . We further choose the origins O and
O′ to coincide at time t = t′ = 0. Your book calls this arrangement the standard
configuration.
. We further choose the origins O and
O′ to coincide at time t = t′ = 0. Your book calls this arrangement the standard
configuration.
Galilean Transformation: Let’s start by giving the classical answer. Time is the same in
both frames, so t = t′. Perpendicular coordinates are the same, so y = y′ and z = z′. Finally,
x′ = x - vt or x = x′ + vt = x′ + vt′. This is called the Galilean transformation (after Galileo
Galilei, the great Italian astronomer):
This is the classical answer and is fine at low velocities much smaller than the speed of light.
But it is not correct relativistically when speeds approach the speed of light. For example, it
does not give time dilation.
Lorentz Transformation: The correct relativistic transformation is called the Lorentz
transformation. We can derive it as follows. Suppose a pulse of light is emitted at t = t′ = 0
from the origin O and O′. (Recall that the origins coincide at t = t′ = 0.) In frame S the
equation of the spherical wave front emitted at t = 0 is
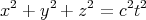 | (28) |
In the frame S′, the equation of the spherical wave front of light must be
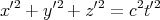 | (29) |
Note that the speed of light c is the same in the two reference frames and so is the same in
Eqs. (28) and (29). If we substitute the Galilean transformation (Eq. (27)) into Eq. (28), we do
not obtain Eq. (29). So let us try a solution of the form
where we have to find the parameters α, ε, δ, and η that will make Eqs. (28) and (29)
consistent. To find these parameters, we can use time dilation and Lorentz contraction to find
that α = η = γ. Then plugging Eqs. (30) into Eq. (29) and demanding that we get Eq. (28), we
obtain the Lorentz transformation: The inverse Lorentz transformation is
This can be viewed as 4 equations and 4 unknowns. In many problems, you are given 3
unknowns and you have to find the fourth.
Let’s take a moment to look at these equations. Space (x) in one frame is a combination of
space (x′) and time (t′) in another inertial frame. Time t in one frame is a combination of
space (x′) and time (t′) in another inertial frame. We think of space and time as
separate things but they are actually mixed together. Space-time is the fabric of the
universe.
Example of the Lorentz Transformation: Length Contraction
Let’s start with the Lorentz transformation and derive the Lorentz contraction. The length ℓ0
of a moving train according to people on the train is
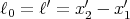 | (33) |
Let’s plug in the Lorentz transformation:
On the ground, two observers measure the coordinates of the front and back of the train at the
same time t. So Δt = 0. They measure the length of the train as
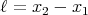 | (35) |
So we can write
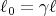 | (36) |
We recover the length contraction equation Eq. (26).
The Velocity-Addition Formula
The classical velocity-addition formula relates the velocity 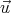 of an object in frame S to the
velocity
of an object in frame S to the
velocity 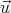 ′ in S′:
′ in S′:
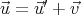 | (37) |
This is Eq. (1). This equation is not valid relativistically. The speed of light in the moving train
(or moving frame of reference) is the same as in S, the ground based frame, but this equation
predicts that light should have different velocities in different frames. Michelson and Morley
showed that light travels at the same velocity in all inertial frames. In section 1.13,
your book starts from the Lorentz tranformation and uses the basic definitions of
velocity
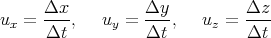 | (38) |
to show that the correct relativistic velocity addition formulas are
Notice that in the nonrelativistic limit when v ≪ c, γ ≈ 1, and we recover the classical velocity
addition formula:
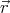 = (x,y,z), we are measuring (x,y,z) with respect to a
given frame of reference. That same position could have different coordinates in another
reference frame. For example, consider the point P in Figure 1. In one frame of reference P has
the coordinates (x = 3,y = 4) while in the other (primed) reference frame, P has the
coordinates (x′ = 1,y′ = 1). The position of P is measured relative to a coordinate
system.
= (x,y,z), we are measuring (x,y,z) with respect to a
given frame of reference. That same position could have different coordinates in another
reference frame. For example, consider the point P in Figure 1. In one frame of reference P has
the coordinates (x = 3,y = 4) while in the other (primed) reference frame, P has the
coordinates (x′ = 1,y′ = 1). The position of P is measured relative to a coordinate
system.
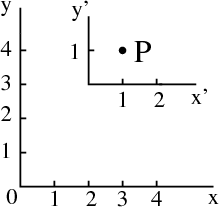
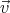 . Each reference frame has an observer. For example, suppose reference frame S is
fixed to the ground and reference frame S’ is fixed to a train moving along the tracks with
constant velocity
. Each reference frame has an observer. For example, suppose reference frame S is
fixed to the ground and reference frame S’ is fixed to a train moving along the tracks with
constant velocity 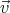 . Each observer is standing still but thinks the other observer is moving. The
person on the train tracks sees the train and the passenger moving at velocity
. Each observer is standing still but thinks the other observer is moving. The
person on the train tracks sees the train and the passenger moving at velocity 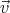 . The
passenger on the train sees the person standing on the tracks go by with velocity
. The
passenger on the train sees the person standing on the tracks go by with velocity
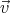 .
.
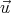
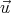 given by the sum of the train
velocity and the velocity of the ball with respect to the train:
given by the sum of the train
velocity and the velocity of the ball with respect to the train:
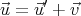
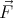 =
= 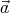
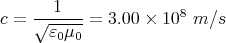
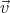 . According to
Eq. (
. According to
Eq. (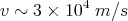
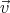 relative to the ground. We’ll call the train frame
relative to the ground. We’ll call the train frame 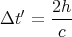
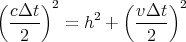
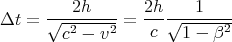
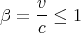
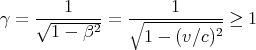
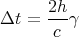
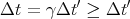
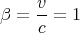
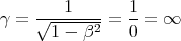
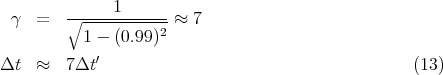
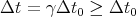
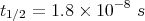
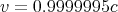
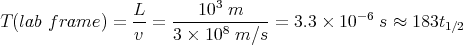

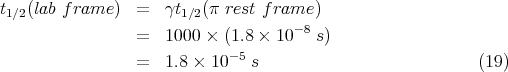
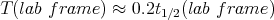
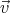 and the other (
and the other (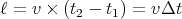

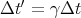

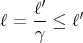
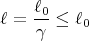
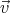 relative to the ground. We choose the
relative to the ground. We choose the 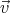 . We further choose the origins
. We further choose the origins 
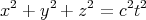
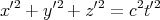



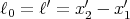
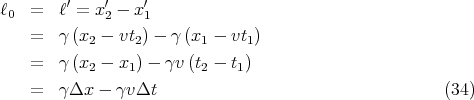
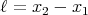
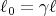
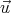 of an object in frame
of an object in frame