Ionic bonding is characterized by electron transfer; one of the reacting atoms loses one or more electrons, and the other atom gains one or more electrons. For example, consider sodium chloride (NaCl, otherwise known as table salt). Sodium is an alkali metal and chlorine is a halogen. To get a complete shell, a sodium atom gives its outer 3selectron to a chlorine atom which otherwise would be one electron short of a complete shell. As a result the sodium ion (Na+) acquires a 1+ charge and the chlorine ion (Cl-) acquires a 1- charge. Positive ions are called cations and negative ions are called anions. We say that chlorine is very electronegative. Electronegativity is a measure of the ability of an atom in a molecule to attract (or hog) electrons to itself.
In covalent bonding electrons are not transferred but are shared;
a covalent bond consists of a pair of electrons (with
opposite spins in a singlet state) shared by two atoms.
An example is the covalent bond formed by two hydrogen atoms in an
H2 molecule. The electrons are attracted by the positive nuclear charge
to the region between the nuclei. The 1s orbitals
overlap to form a sigma bonding orbital (![]() ). The spatial
part of the sigma bonding orbital
). The spatial
part of the sigma bonding orbital
![]() is a symmetric linear combination of the 1s orbitals:
is a symmetric linear combination of the 1s orbitals:
| (1) |
There is also
a sigma antibonding orbital (
![]() ) which is spatially an antisymmetric
linear combination of the 1s orbitals:
) which is spatially an antisymmetric
linear combination of the 1s orbitals:
| (2) |
Notice that the number of single electron states
is conserved in bonding. We started with 2 individual atoms, each with
a 1s orbital. That makes a total of 4 single electron states, counting
spin. Covalent bonding leads to 2 sigma orbitals
(![]() and
and
![]() ) which have a total of 4 single particle states.
If we try to form a helium molecule, He2, we would put the
two 1s orbitals together and form the
) which have a total of 4 single particle states.
If we try to form a helium molecule, He2, we would put the
two 1s orbitals together and form the ![]() and
and
![]() orbitals. Then we would fill them with the 4 helium electrons. The
energy gained by putting two electrons in the sigma bonding orbital
is lost by putting the other two electrons in the sigma antibonding
orbital. So He2 is unstable and no bond is formed. Helium is
a noble gas and doesn't need other electrons to complete its atomic orbital
shell.
orbitals. Then we would fill them with the 4 helium electrons. The
energy gained by putting two electrons in the sigma bonding orbital
is lost by putting the other two electrons in the sigma antibonding
orbital. So He2 is unstable and no bond is formed. Helium is
a noble gas and doesn't need other electrons to complete its atomic orbital
shell.
The molecular orbitals derived from the overlap of 2p atomic orbitals are
slightly more complicated. The three 2p orbitals of an atom are directed
along the Cartesian coordinates x, y, and z. If we consider that
a diatomic molecule is formed by the atoms approaching each other
along the x axis, the px atomic orbitals approach each other head
on and overlap to produce ![]() bonding and
bonding and
![]() antibonding molecular orbitals. All sigma orbitals are symmetrical
about the internuclear axis; the
antibonding molecular orbitals. All sigma orbitals are symmetrical
about the internuclear axis; the ![]() and
and
![]() orbitals have shapes that are similar to those of the
orbitals have shapes that are similar to those of the ![]() and
and
![]() orbitals.
orbitals.
In the formation of a diatomic molecule, the pz atomic
orbitals approach each other side to side and produce pi (![]() )
bonding and antibonding molecular orbitals.
)
bonding and antibonding molecular orbitals. ![]() orbitals are not
symmetrical about the internuclear axis. The electron density
of a
orbitals are not
symmetrical about the internuclear axis. The electron density
of a ![]() bonding orbital is zero in a plane that includes both
nuclei of the molecule, but charge is concentrated in two regions that lie
above and below this plane and between the two nuclei. The
bonding orbital is zero in a plane that includes both
nuclei of the molecule, but charge is concentrated in two regions that lie
above and below this plane and between the two nuclei. The ![]() orbital reduces electronic density in the internuclear region.
orbital reduces electronic density in the internuclear region.
The py orbitals also approach each other sideways. Consequently
another set of ![]() and
and ![]() molecular orbitals, which lie
at right angles to the set resulting from the overlap of pzorbitals, can be produced. The two
molecular orbitals, which lie
at right angles to the set resulting from the overlap of pzorbitals, can be produced. The two ![]() orbitals are degenerate
(have equal energy), and the two
orbitals are degenerate
(have equal energy), and the two
![]() orbitals are degenerate.
Six molecular orbitals, therefore, arise from the two sets of porbitals-one
orbitals are degenerate.
Six molecular orbitals, therefore, arise from the two sets of porbitals-one ![]() , one
, one
![]() , two
, two ![]() , and
two
, and
two
![]() .
.
In forming a diatomic molecule, the ![]() and
and
![]() orbitals
are lower in energy than the orbitals formed from the 2p orbitals.
So the
orbitals
are lower in energy than the orbitals formed from the 2p orbitals.
So the ![]() and
and
![]() orbitals will be occupied before
the
orbitals will be occupied before
the ![]() or
or ![]() orbitals are.
orbitals are.
Pure ionic bonding and pure covalent bonding are seldom encountered.
Most bonds have intermediate character, although many bonds are
predominantly either ionic or covalent. In heteronuclear, diatomic
molecules the clouds of the bonding orbitals are distorted so that more
electronic charge is located around the more electronegative atom than
around the other atom; antibonding orbitals have their largest
electron density in the regions close to the less electronegative
atom. The molecular orbital wavefunction has the form
| (3) |
In some molecules which consist of more than 2 atoms, there can be multicenter
or delocalized bonding in which some of the bonding electrons bond more
than 2 atoms. One example is the ![]() bonding found in benzene which
consists of 6 carbon atoms in a ring. A carbon atom has 4 valence
electrons, so it wants to form 4 bonds to have a filled shell. In benzene
each carbon atom forms one bond with a hydrogen atom and 3 bonds with
its neighboring 2 carbon atoms.
bonding found in benzene which
consists of 6 carbon atoms in a ring. A carbon atom has 4 valence
electrons, so it wants to form 4 bonds to have a filled shell. In benzene
each carbon atom forms one bond with a hydrogen atom and 3 bonds with
its neighboring 2 carbon atoms.
The ultimate in delocalized bonding is metallic bonding. In a metal the atoms contribute their valence electrons to the collective whole. As a result the electrons do not belong to any specific atom, but have wavefunctions that extend throughout the whole system. These conduction electrons are responsible for holding the metal together. This is metallic bonding.
I want to mention 2 models of the nucleus. One is called the liquid drop model and the other is called the nuclear shell model. The liquid drop model is based on two properties that are common to all except the lightest nuclei, (1) the interior mass densities are approximately the same and (2) the binding energy per nucleon is approximately 8 MeV. The liquid droplet model views the nucleus as a tiny incompressible drop of liquid with the constituents being nucleons. In physics a ``gas'' is used to describe a bunch of noninteracting particles whose energy consists only of kinetic energy, and a liquid is a ``gas'' of interacting particles. The liquid droplet model views the nucleons largely as classical particles.
| (4) |
| (5) |
| (6) |
Besides predicting the magic numbers, the shell model can also
predict the total angular momentum I of the ground states of
almost all the nuclei. (The total angular momentum of the
nucleus is often referred to as its spin.)
It turns out that pairs of nucleons of the
same type (e.g., pairs of protons) strongly tend to combine with one
another to yield zero angular momentum. Thus all even-even nuclei
have I=0. ``Even-even nuclei'' means nuclei with even numbers
of protons and even numbers of neutrons. Nucleons of the same kind
tend to pair because it increases their overlap and enables them
to take advantage of the short range attractive strong force.
A simple example is the fact that 2 fermions in a singlet state,
which is antisymmetric in spin space, have a symmetric spatial wavefunction
which has more overlap than its antisymmetric spatial counterpart. Now
consider the case of odd-A nuclei which have an even number
of nucleons of one kind and an odd number of the other. All the
nucleons pair to yield zero angular momentum except the odd nucleon.
The angular momentum of the odd-A nucleus should just be that
of the odd nucleon, and indeed this is the case for virtually all
odd-A nuclei whose spin is known. Further the same argument applied
to (presumably unstable)
odd-odd nuclei suggests that their angular momentum ought to be
some combination of the angular momenta of the two odd nucleons.
Again this is observed to be the case, but, of course,
this test is not nearly as definitive as the first one.
Odd-odd nuclei have an odd number of neutrons and an odd number of
protons. An odd-odd nucleus should be
unstable because it can become an even-even
nucleus of lower energy by having one of its neutrons decay into
a proton. A neutron can decay into a proton, an electron, and an
electron antineutrino in a process called beta decay.
| (7) |
The shell model has also met with considerable success in providing a semiquantitative description of many of the properties of the low-lying excited states of most odd-A nuclei.
Another interesting phenomenon for which the shell model provides an
illuminating semiquantitative explanation is that of nuclear
isomerism. In the study of the excited states of nuclei it is
found that certain nuclei can exist for quite extended periods of time
in an excited state, from which they often finally decay by
![]() -ray emission. Such states may have decay lifetimes ranging
up to many days. The nuclei which can exist in these so-called
metastable states tend to be those having a nearly closed shell
configuration of nucleons. The explanation of the long lifetimes
of these metastable states lies in the fact that the ground state
and the first excited state differ in angular momentum by several
units of
-ray emission. Such states may have decay lifetimes ranging
up to many days. The nuclei which can exist in these so-called
metastable states tend to be those having a nearly closed shell
configuration of nucleons. The explanation of the long lifetimes
of these metastable states lies in the fact that the ground state
and the first excited state differ in angular momentum by several
units of ![]() . Thus, many of the lower-order transitions, such
as electric dipole, magnetic dipole, and electric quadrupole,
are forbidden, so that a transition of very high multipole order
may be required. The probability of transition rapidly becomes smaller
with increasing multipole order, so that a long lifetime for the state
results.
. Thus, many of the lower-order transitions, such
as electric dipole, magnetic dipole, and electric quadrupole,
are forbidden, so that a transition of very high multipole order
may be required. The probability of transition rapidly becomes smaller
with increasing multipole order, so that a long lifetime for the state
results.
Another nuclear property for which the shell model provides an explanation
is the parity of the ground state. Recall that parity
refers to whether the spatial part of the wavefunction changes
sign when
![]() . By the arguments used in
connection with angular momenta, the ground state parity of even-even
nuclei should be even, and that of odd-A nuclei should correspond to
. By the arguments used in
connection with angular momenta, the ground state parity of even-even
nuclei should be even, and that of odd-A nuclei should correspond to
![]() where
where ![]() is the orbital angular momentum of the
odd nucleon. This rule is observed to lead to the correct parities
for virtually all cases.
is the orbital angular momentum of the
odd nucleon. This rule is observed to lead to the correct parities
for virtually all cases.
So we can see that the nuclear shell model is quite good at explaining many of the properties of nuclei.
Niels Bohr and John Wheeler produced a general theory of fission
in 1939. They predicted that only the rare isotope of uranium,
U-235, would be fissionable by slow neutrons. The reason is that
U-235 has an odd number of neutrons. The incoming neutron
binds with the odd neutron to form a neutron pair
and the energy gained from this binding (of order an MeV) helps
the nucleus to deform and break apart. However, U-238 has an even
number of neutrons and doesn't gain the extra binding
energy from forming a pair. So the energy to deform and fission
the U-238 nucleus
comes from the kinetic energy of the incoming neutron.
Nier showed experimentally that indeed U-235 can be fissioned
by slow neutrons while U-238 requires neutrons of about 1 MeV.
Since the nuclear cross section goes as 1/E where E is the
energy of the incoming neutron, slower neutrons have a bigger
chance of hitting a nucleus than faster neutrons. (The cross
section ![]() = decay rate/(incoming flux of particles).) So
it's easier to cause fission in U-235 than in U-238.
In nuclear reactors graphite is used to slow the fission neutrons,
originally emitted at about 1 MeV energy, down to thermal energies
which is less than 1 eV. Graphite is a form of carbon which
absorbs very few neutrons. Heavy water works even better but is
harder to come by. The heat from water used to cool the graphite is
used to make steam which in turns runs turbines and generates
electricity in a nuclear power plant. Neutron absorbers, like rods of boron,
are used to control the reaction. The rods are inserted to slow
the reaction and taken out if the reaction is too going to slowly.
= decay rate/(incoming flux of particles).) So
it's easier to cause fission in U-235 than in U-238.
In nuclear reactors graphite is used to slow the fission neutrons,
originally emitted at about 1 MeV energy, down to thermal energies
which is less than 1 eV. Graphite is a form of carbon which
absorbs very few neutrons. Heavy water works even better but is
harder to come by. The heat from water used to cool the graphite is
used to make steam which in turns runs turbines and generates
electricity in a nuclear power plant. Neutron absorbers, like rods of boron,
are used to control the reaction. The rods are inserted to slow
the reaction and taken out if the reaction is too going to slowly.
To understand this in more detail, consider a
set of identical nuclei of spin I and magnetic moment
![]() , where gnis the dimensionless nuclear g-factor (typically
, where gnis the dimensionless nuclear g-factor (typically ![]() ),
),
![]() is the nuclear magneton, and
is the nuclear magneton, and ![]() is the gyromagnetic ratio (
is the gyromagnetic ratio (
![]() ). (In
). (In
![]() we just have the proton mass MP rather than the
mass of all the nucleons because it's usually the odd nucleon
that determines
we just have the proton mass MP rather than the
mass of all the nucleons because it's usually the odd nucleon
that determines ![]() .) We start
with a simple quantum mechanical view of resonance theory. If we
apply a magnetic field
.) We start
with a simple quantum mechanical view of resonance theory. If we
apply a magnetic field ![]() , the Hamiltonian is
, the Hamiltonian is
| (8) |
| (9) |
| (10) |
lec7levels.eps
We can get transitions between the levels by applying an alternating
rf field perpendicular to the static field. (rf stands for radio
frequency.) We get a transition if
| (11) |
| (12) |
To see why the transitions are between adjacent levels, notice that
the rf field is given by
| (14) |
| (15) |
| (16) |
| (17) |
Note that Planck's constant has disappeared from the resonance condition,
implying that a classical picture could also be used. We will describe
such a picture, but first, some numbers. Note that
![]() and
and
![]() . Since
. Since
![]() , nuclear numbers
differ from electronic numbers by about 103. Thus
, nuclear numbers
differ from electronic numbers by about 103. Thus
![]() Hz/Tesla and
Hz/Tesla and
![]() Hz/Tesla. Electronic systems have a
resonance at
Hz/Tesla. Electronic systems have a
resonance at
![]() MHz (
MHz (
![]() cm which is in the
microwave region), whereas nuclear systems typically resonate at
10 MHz (a radio frequency) for
cm which is in the
microwave region), whereas nuclear systems typically resonate at
10 MHz (a radio frequency) for
![]() to 10,000 Gauss.
to 10,000 Gauss.
Classical Treatment A magnetic moment ![]() in a magnetic
field
in a magnetic
field ![]() experiences a torque
experiences a torque
![]() . Thus
. Thus
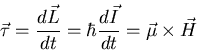 |
(18) |
| (19) |
lec7precess.eps
Now let's examine the effect of the alternating magnetic field.
![]() is most readily analyzed by breaking it
into two rotating components, each of amplitude Hox, one rotating
clockwise and the other counterclockwise. We denote the rotating
fields by
is most readily analyzed by breaking it
into two rotating components, each of amplitude Hox, one rotating
clockwise and the other counterclockwise. We denote the rotating
fields by ![]() and
and ![]() :
:
| (20) |
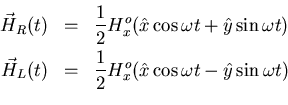
lec7Hx.eps
Let's suppose that
![]() . This is the resonance condition.
In the reference frame rotating with the magnetic moment of the nucleus,
HL looks like a static field pointing along the x axis,
while HR is rotating at
. This is the resonance condition.
In the reference frame rotating with the magnetic moment of the nucleus,
HL looks like a static field pointing along the x axis,
while HR is rotating at ![]() and averages to zero.
So we can ignore HR.
and averages to zero.
So we can ignore HR.
So in the rotating frame
at resonance (
![]() ), the magnetic moment sees
a static magnetic field
), the magnetic moment sees
a static magnetic field
![]() pointing along the x axis. So if
pointing along the x axis. So if ![]() initially points along
the
initially points along
the ![]() , then it will precess in the y-z plane about the
x axis. If we turn on H1 for a short time tw, the moment
precesses through an angle
, then it will precess in the y-z plane about the
x axis. If we turn on H1 for a short time tw, the moment
precesses through an angle
![]() . If
. If
![]() ,
the pulse inverts
,
the pulse inverts ![]() . This is called a ``180 degree pulse'' or
``
. This is called a ``180 degree pulse'' or
``![]() pulse.'' If
pulse.'' If
![]() ,
, ![]() is rotated until it
lies parallel to
is rotated until it
lies parallel to ![]() . This is called a ``90 degree pulse'' or
a ``
. This is called a ``90 degree pulse'' or
a ``![]() pulse.'' After H1 is turned off, the moment remains
at rest in the rotating frame, and hence precesses in the laboratory
frame in a plane normal to the field. This suggests a way of observing
magnetic resonance. Put the sample in a solenoid. Pulse the solenoid
with an rf field that tips the nuclear spins by 90o. Then as the
spins precess in the x-y plane, they produce a time-varying flux
through the coil that induces an observable emf according to Faraday's
law.
pulse.'' After H1 is turned off, the moment remains
at rest in the rotating frame, and hence precesses in the laboratory
frame in a plane normal to the field. This suggests a way of observing
magnetic resonance. Put the sample in a solenoid. Pulse the solenoid
with an rf field that tips the nuclear spins by 90o. Then as the
spins precess in the x-y plane, they produce a time-varying flux
through the coil that induces an observable emf according to Faraday's
law.
coil.eps
What we have suggested so far would indicate that the induced emf
would persist indefinitely, but in practice, the interactions of the
spins with their surroundings cause a decay. Let ![]() denote the
relaxation time. Then
denote the
relaxation time. Then ![]() milliseconds in liquids and
milliseconds in liquids and
![]() s in solids. Even during that short time, there
are many precession periods. What we have described is the observation
of the ``free induction decay'' (i.e., free of H1).
s in solids. Even during that short time, there
are many precession periods. What we have described is the observation
of the ``free induction decay'' (i.e., free of H1).
T1decay.eps
We have been considering a uniform field
![]() . To give
the system some spatial resolution, one can vary the static field spatially
by putting on a field gradient. Then only those spins that are
located where
. To give
the system some spatial resolution, one can vary the static field spatially
by putting on a field gradient. Then only those spins that are
located where
![]() will give a strong signal.
will give a strong signal.
spinecho.eps
If the spins initially are aligned along the z axis, the ![]() pulse
puts them in the x-y plane where they dephase due to field inhomogeneities
and spin-spin interactions. The
pulse
puts them in the x-y plane where they dephase due to field inhomogeneities
and spin-spin interactions. The ![]() pulse refocuses the spins and
they produce an echo a time
pulse refocuses the spins and
they produce an echo a time ![]() later.
later.
rephase.eps