


Next: About this document ...
Physics 224 Fall 1998
Phenomenology due 11:00 am Thursday Nov. 5
PROBLEM SET 5
Oct. 30 Colloquium:
``On the Geometry of 'Time Travel' in Godel's Universe''
Professor David Malament, University of Chicago
3 pm, 101 Rowland Hall (formerly PS I)
- 1.
- What will your final report be on? To find possible topics,
look at Eisberg and Resnick, The New Physics, or Scientific
American.
- 2.
- In the transition
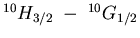 ,
how many lines will
appear in the Zeeman pattern? Explain your reasoning by listing the
allowed transitions.
,
how many lines will
appear in the Zeeman pattern? Explain your reasoning by listing the
allowed transitions.
- 3.
- Eisberg and Resnick problem 12.22(a).
- 4.
- How does the transition temperature
TC depend on the number of particles N if E=pc for Bose condensation?
(Hint:You don't have to evaluate any integrals. Just try scaling, i.e.,
make the variables in the integral dimensionless. Your answer should be of
the form
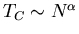 .
Find
.
Find  .)
.)
- 5.
- In the Weiss (mean-field) theory of ferromagnetism the Gibbs
free energy (
G=E(M)-HM-TS, where H is the externally applied
magnetic field, M is the magnetization, E is the internal energy,
and S is the entropy) has the form
|
G=Go(T)+a(T)M2+b(T)M4+O(M6)-MH
|
(1) |
where Go(T) is independent of M, and where the coefficient
b(T) is a slowly varying function of T but a(T) is of the
form
ao(T-TC), TC being the critical temperature in Weiss
theory. Assume that T is close to TC and
that M is small. Using the fact that in thermal equilibrium M will take
the value which minimizes G, find (a) the equilibrium value of Mfor H=0, for T>TC and T<TC; (b) the
form of M at TC as a function of H; (c) the zero-field
differential susceptibility
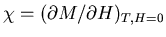 for T>TC and T<TC; and (d) the discontinuity in the
specific heat at constant H (
for T>TC and T<TC; and (d) the discontinuity in the
specific heat at constant H (
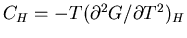 )
at the point T=TC and H=0. In other words find the difference
between the limits of
CH(T,H=0) as
)
at the point T=TC and H=0. In other words find the difference
between the limits of
CH(T,H=0) as
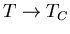 from
above and from below.
from
above and from below.



Next: About this document ...
Clare Yu
1998-10-28