


Next: About this document ...
Physics 224 Fall 2002
Discoveries and Inventions of Modern Physics due 11:00 am Tuesday Oct. 22
PROBLEM SET 3
No Colloquium on Oct. 17
- 1.
- Eisberg and Resnick: 7.4
- 2.
- Identify the atoms that have the following ground state electronic
configurations in their outer shell or shells: (a)
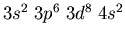 ,
(b)
,
(b)
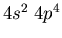 (c)
(c)
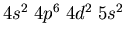 (d)
(d)
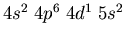 ,
(e)
,
(e)
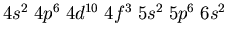 .
.
- 3.
- Show that the multiplicity of a level, defined as the number
of different J-values that can be formed from given L and Svalues, is 2L+1 or 2S+1, whichever is smaller.
- 4.
- What are the values of L, S, and J and the multiplicities
of the levels having the following term designations: 1S0, 3D2,
4P5/2, 2F7/2,
6I13/2?
- 5.
- What types of terms can result from the following values of Land S? (Answer in spectroscopic notation.) (a) L=1, S=1/2(b) L=3, S=1, (c) L=2, S=7/2, (d) L=5, S=3/2.
(Partial answer: (a) 2P1/2, 2P3/2).
- 6.
- What spectral terms result from an electron configuration
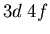 ,
assuming LS coupling?
,
assuming LS coupling?
- 7.
- In the transition
,
how many lines will
appear in the Zeeman pattern? Explain your reasoning by listing the
allowed transitions.
Clare Yu
2002-10-13