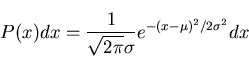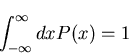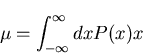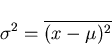Physics 214A   Winter 2009

Statistical Physics 		due 9:30 am Tuesday, January 13

PROBLEM SET 1

Reading: Chapter 1 (especially sections 1.1-1.6 and last paragraph of page 39) and Chapter 2 in Reif.

Problems:

Hint: Notice that for analytical calculations, there are many helpful mathematical appendices in Reif.

1. Show explicitly that the following identities are correct for the Gaussian function
   
   $$P(x)dx=\frac{1}{\sqrt{2\pi}\sigma}e^{-(x-\mu)^2/2\sigma^2}dx$$
   
   
   1. Normalization
      
      $$\int^{\infty}_{-\infty} dx P(x)=1$$
      
      

   2. Mean or average value
      
      $$\mu=\int^{\infty}_{-\infty} dx P(x)x$$
      
      

   3. Variance or second moment of the distribution
      
      $$\sigma^2=\overline{(x-\mu)^2}$$
      
      

2. Reif 1.9
3. Reif 1.10
4. Reif 1.11
5. Reif 1.19
6. Reif 2.1
7. Poisson Distribution in Molecular Biology The classical simple system of molecular biology is the infection of E. coli B bacteria with viruses called bacteriophage. A virus particle can only multiply inside a bacterium. The virus enters the bacterium and multiplies with the cell. After about 20 minutes at 37 C, the cell wall of the bacterium breaks up. This destroys the bacterium and releases approximately 100 new virus particles. Suppose that we have 100 test tubes filled with E. coli bacteria in a nutrient solution. All the test tubes appear cloudy because the bacteria quickly multiply and their dimensions (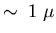$\sim\;1\;\mu$m) are favorable for scattering light. If a single virus particle is added to a test tube that contains E. coli, and then the tube is incubated overnight, the result is a clear test tube. This is because the virus multiplies, destroys the bacteria and makes bacterial fragments that are too small to scatter light. If 2 or more viruses are present initially in a tube, the result is indistinguishable from one virus particle-the tube is clear.

   Suppose that 1 ml from a large vessel of virus solution is added to each of 100 tubes of bacteria, and that after incubation 39 of these tubes are found to be cloudy. What is the average number of virus particles in 1 ml of the original virus solution?