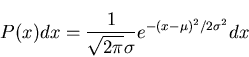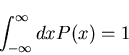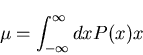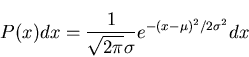
- (a)
- Normalization
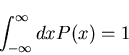
- (b)
- Mean or average value
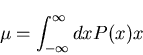
- (c)
- Variance or second moment of the distribution
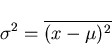
Physics 115A Spring 2001
Statistical Physics due 12:30 pm Thursday, April 12
Reading: Chapter 1 (especially sections 1.1-1.6 and last paragraph of
page 39) and Chapter 2 in Reif.
Hint: Notice that there are many helpful mathematical appendices in Reif.