LECTURE 9

Statistical Mechanics

Basic Methods

We have talked about ensembles being large collections of copies or clones of a system with some features being identical among all the copies. There are three different types of ensembles in statistical mechanics.

If the system under consideration is isolated, i.e., not interacting with any other system, then the ensemble is called the microcanonical ensemble. In this case the energy of the system is a constant.
If the system under consideration is in thermal equilibrium with a heat reservoir at temperature T, then the ensemble is called a canonical ensemble. In this case the energy of the system is not a constant; the temperature is constant.
If the system under consideration is in contact with both a heat reservoir and a particle reservoir, then the ensemble is called a grand canonical ensemble. In this case the energy and particle number of the system are not constant; the temperature and the chemical potential are constant. The chemical potential is the energy required to add a particle to the system.

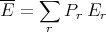
The most common ensemble encountered in doing statistical mechanics is the canonical ensemble. We will explore many examples of the canonical ensemble. The grand canonical ensemble is used in dealing with quantum systems. The microcanonical ensemble is not used much because of the difficulty in identifying and evaluating the accessible microstates, but we will explore one simple system (the ideal gas) as an example of the microcanonical ensemble.

Microcanonical Ensemble

Consider an isolated system described by an energy in the range between E and E + δE, and similar appropriate ranges for external parameters x_α. To illustrate a microcanonical ensemble, consider only the energy parameter. Let E_r be the total energy of the rth microstate. Also let P_r be the probability of the system being in the rth microstate. The average energy is

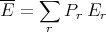E- = ∑ P E r r r

(1)

where the sum is over the accessible microstates. From the postulates of statistical mechanics that all microstates are equally probable, the probability of the system being in any microstate is a constant as long as the total energy is in the range E to E + δE. Assume there are ν such states, then

1 Pr = -- ν

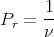(2)

The average value of any property of the system is

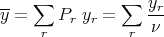-- ∑ ∑ yr y = Pr yr = ν r r

(3)

where y_r is the value of the property y when the system is in the rth microstate. The difficulty is that identifying the correct set of microstates is exceedingly difficult. If we think of phase space as consisting of all possible microstates of the system with all possible energies, then the microcanonical ensemble consists of the subset of phase space with microstates that have energy between E and E + δE. Picking out these states is difficult. For example consider an ideal gas. Let each gas particle be a “system”. Each system or particle is isolated and doesn’t interact with anything. The microcanonical ensemble would consist of those particles with kinetic energy between E and E + δE, i.e., it would consist of only those particles with a certain velocity. We could only sum over those particles, not all the particles. Picking out these particles is a pain.

Canonical Ensemble

The most common situation encountered in statistical mechanics is that of a system in thermal contact with a heat reservoir at constant temperature T. In equilibrium the system is also at temperature T. The system under consideration may be a small part of a larger system, for example, a 1 gram block of copper immersed in a container of liquid helium at 4.2 K.

Assume that system A is in thermal contact with a heat reservoir A^′. Thermal contact means that only heat can be exchanged between A and A^′. The energy of system A cannot be specified since it will fluctuate as heat is exchanged randomly between A and A^′ (but E will be well defined). Let E_r be the energy of a microstate of A. Then

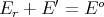E + E′ = Eo r

(4)

where E^′ is the energy of the heat reservoir A^′ and E^o is the total energy of the combined system A and A^′. The probability P_r of A being in microstate r is proportional to the number Ω^′(E^′ = E^o - E_r) of microstates of the reservoir:

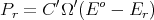Pr = C ′Ω′(Eo - Er )

(5)

where C^′ is a constant determined by the normalization condition:

∑ Pr = 1 r

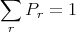(6)

Now assume E_r ≪ E^o (i.e., assume that A^′ is a heat reservoir) and expand about E^′ = E^o:

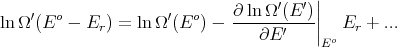′ ′ || lnΩ ′(Eo - Er) = ln Ω′(Eo) - ∂-lnΩ-(E--)|| Er + ... ∂E ′ |Eo

(7)

where we used ′ o
(E - E ) = -E_r. But

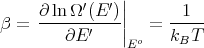| ∂ ln Ω′(E ′)|| 1 β = ------′---|| = ----- ∂E Eo kBT

(8)

where T is the temperature of the reservoir. Thus

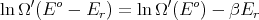′ o ′ o ln Ω (E - Er ) = lnΩ (E ) - βEr

(9)

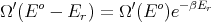Ω ′(Eo - Er) = Ω ′(Eo )e-βEr

(10)

Thus

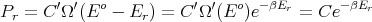P = C ′Ω ′(Eo - E ) = C ′Ω ′(Eo )e-βEr = Ce -βEr r r

(11)

where

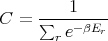C = ∑---1---- r e- βEr

(12)

Finally

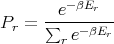-βE P = ∑-e---r-- r r e-βEr

(13)

This probability distribution is sometimes called the Boltzmann distribution. It tells us the probability that a microstate with energy E_r will be occupied. Notice that if E_r < k_BT, then there is a good chance that the state will be occupied. But if E_r is large compared to the temperature, then the chance that the rth state is occupied is exponentially small.

The average value of any parameter y is given by

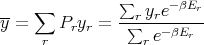∑ -- ∑ r yre-βEr y = Pryr = -∑--e-βEr-- r r

(14)

where y_r is the value of the parameter y in the rth state. For example, the mean energy is

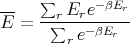-- ∑ E e-βEr E = -∑r--r--βE--- r e r

(15)

The denominator arises quite frequently. So let

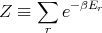∑ -βEr Z ≡ e r

(16)

Z is called the partition function. It acts like a generating function. For example,

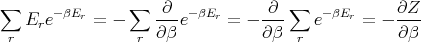∑ - βEr ∑ -∂- -βEr -∂- ∑ -βEr ∂Z-- Ere = - ∂β e = - ∂ β e = - ∂ β r r r

(17)

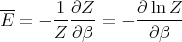-- 1-∂Z-- ∂ lnZ- E = - Z ∂ β = - ∂β

(18)

The partition function Z is quite useful and we can use it to generate all sorts of information about the statistical mechanics of the system.

The advantage of the canonical ensemble should now be apparent. The sum is over all the microstates of the system. We don’t have the difficulty of finding only those microstates whose energy lies within some specified range.

Let us also calculate the dispersion (ΔE)² of the energy:

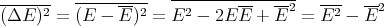------- ---------- ---------------- (ΔE )2 = (E - E)2 = E2 - 2EE--+ E2 = E2-- E2

(19)

We have already computed E. We need now to compute E²:

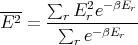--- ∑r E2re-βEr E2 = -∑-----βEr-- r e

(20)

But

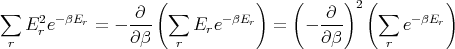∑ ∂ (∑ ) ( ∂ )2 ( ∑ ) E2re- βEr = - --- Ere-βEr = - --- e-βEr r ∂β r ∂β r

(21)

And from the definition of the partition function Z

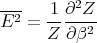--- 2 E2 = 1-∂-Z- Z ∂β2

(22)

This can be rewritten as

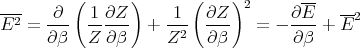--- ∂ ( 1∂Z ) 1 ( ∂Z )2 ∂E- --2 E2 = --- ------ + --2 ---- = - ----+ E ∂ β Z ∂β Z ∂ β ∂β

(23)

Finally we obtain

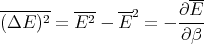------- --- -- -- (ΔE )2 = E2 - E2 = - ∂-E- ∂β

(24)

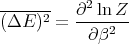------- 2 (ΔE )2 = ∂--ln-Z- ∂β2

(25)

We can relate this to the specific heat at constant volume in the following way. Recall that

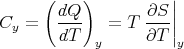( ) | dQ- ∂S-|| Cy = dT = T ∂T || y y

(26)

Let y = V , then at constant volume

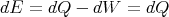dE = dQ - dW = dQ

(27)

since dW = pdV = 0. Thus

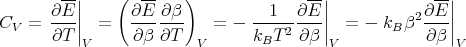--| ( -- ) --| --| ∂E-|| ∂E--∂β- --1---∂E-|| 2∂E-|| CV = ∂T || = ∂ β ∂T = - k T 2∂β || = - kBβ ∂β || V V B V V

(28)

But

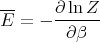-- ∂-lnZ- E = - ∂β

(29)

Therefore

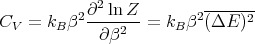2∂2-ln-Z- 2-----2- CV = kBβ ∂ β2 = kBβ (ΔE )

(30)

Notice that the specific heat is related to the fluctuations in the internal energy or, equivalently, to the width of the distribution of E. In a numerical simulation, one way to calculate the specific heat is to calculate (ΔE)².

We can also use Z to generate the mean generalized force X. Suppose now that we change some macroscopic parameter x. Then the energy changes by the amount

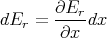∂Er- dEr = ∂x dx

(31)

and the macroscopic work done by the system is

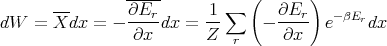----- ( ) --- ∂Er 1 ∑ ∂Er - βEr dW = Xdx = - ∂x--dx = Z- - -∂x- e dx r

(32)

Now note that in the numerator

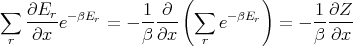( ) ∑ ∂Er - βE 1 ∂ ∑ - βE 1 ∂Z ----e r = - ----- e r = - ------ r ∂x β ∂x r β ∂x

(33)

Substituting in (32), we obtain

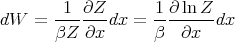-1--∂Z-- -1∂-lnZ- dW = βZ ∂x dx = β ∂x dx

(34)

Recall that

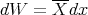dW = Xdx

(35)

where X is the generalized force associated with the parameter x:

----- X--≡ - ∂Er- ∂x

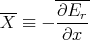(36)

Thus, comparing (34) and (35) leads to

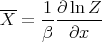--- 1-∂ lnZ- X = β ∂x

(37)

If x is the volume, then X is the pressure p:

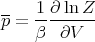-- 1-∂-ln-Z- p = β ∂V

(38)

Now let’s derive a relation between S and Z. Note that Z is a function of both β and x. Thus

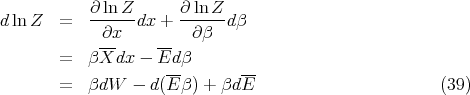
∂ ln Z ∂ lnZ dln Z = --∂x--dx + --∂β--dβ --- -- = βXdx - Ed-β -- = βdW - d(E β) + βdE (39)

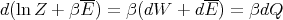-- -- d(lnZ + βE ) = β(dW + dE) = βdQ

(40)

But since

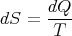dQ dS = --- T

(41)

we obtain

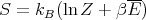-- S = kB (ln Z + β E)

(42)

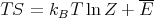-- T S = kBT lnZ + E

(43)

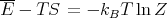-- E - T S = - kBT ln Z

(44)

Recall that in thermodynamics F = E - TS where F is the Helmholtz free energy. Hence

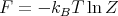F = - kBT ln Z

(45)

Z = e-βF

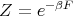(46)

This equation forms the bridge between the canonical ensemble of statistical mechanics and thermodynamics. We can use it to relate the microscopics of the system to the macroscopic parameters that we deal with in thermodynamics.

Notice that since

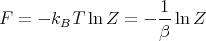1- F = - kBT lnZ = - β lnZ

(47)

we can write the mean pressure as

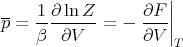| -- 1-∂ ln-Z ∂F-|| p = β ∂V = - ∂V || T

(48)

We obtained this previously using

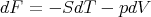dF = - SdT - pdV

(49)

We can also relate the specific heat to the Helmholtz free energy:

F = E - T S

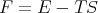(50)

Recall that

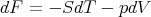dF = - SdT - pdV

(51)

implies that

( ∂F ) S = - ---- ∂T V

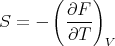(52)

We got this when we derived F = F(T,V ) using a Legendre transformation. We can obtain the specific heat C_V using

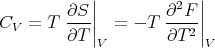|| 2 || C = T ∂S-|| = - T ∂-F-|| V ∂T |V ∂T 2|V

(53)

This is equivalent to eq. (30).

We now see that the partition function contains the information about the system. Most quantities of interest are obtained from the appropriate derivatives of Z. The real task in statistical mechanics is to calculate the partition function. Once that is done, all that remains is differentiation.

Grand Canonical Ensemble

Suppose that the system under consideration is in contact with both a particle and energy reservoir. In this case both energy and particle number can be exchanged with the reservoir. In this situation neither the total energy nor the particle number of the system is constant. Two examples of such systems are a liter of air within a larger volume of air, and a 1 cm³ sample of copper within a larger block of copper. For mathematical reasons quantum mechanical systems are most easily treated when in contact with both a heat and particle number reservoir.

Assume that system A can exchange both energy and particles with system A^′. Assume

′ o E + E = E N + N ′ = N o (54)

Let Ω^′(E^′,N^′) be the number of microstates accessible to the reservoir A^′ when it has energy E^′ and contains N^′ particles. The probability P_r of finding A in the microstate r is

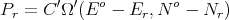P = C ′Ω ′(Eo - E ,N o - N ) r r r

(55)

where C^′ is a constant. Since both E_r ≪ E^o and N_r ≪ N^o,

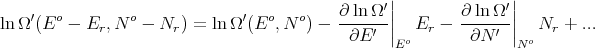| | ′ o o ′ o o ∂-lnΩ-′|| ∂-lnΩ-′|| ln Ω (E - Er, N - Nr) = lnΩ (E ,N ) - ∂E ′ || Er - ∂N ′ || Nr + ... Eo No

(56)

Let

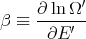∂-ln-Ω-′ β ≡ ∂E ′

(57)

and

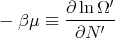∂-ln-Ω-′ - β μ ≡ ∂N ′

(58)

where μ is called the chemical potential. Note that both T and μ are properties of the reservoir and not the system A. If we use the chain rule, then

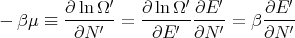∂-ln-Ω′- ∂-lnΩ-′∂E-′ ∂E-′ - βμ ≡ ∂N ′ = ∂E ′ ∂N ′ = β ∂N ′

(59)

This implies that

∂E-′ μ = - ∂N ′

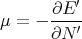(60)

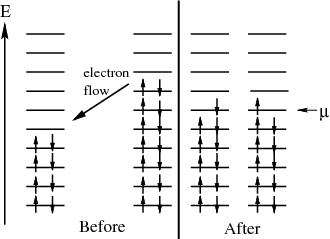
This is consistent with the statement that the chemical potential is the energy required to add a particle or the difference in energy between having N^′ and N^′ + 1 particles. One way to think about chemical potential is in terms of energy levels of 2 pieces of metal. If the two pieces have different numbers of electrons, when they are put into contact, electrons will flow from one to the other because electrons in a higher energy level in one metal can lower their energy by going to a lower level in the other metal. This flow continues until the electrons are filled up to the same level. This “level” is the chemical potential.

chempot.eps

Back to (56):

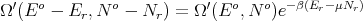′ o o ′ o o -β(Er-μNr) Ω (E - Er,N - Nr) = Ω (E ,N )e

(61)

and

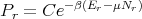P = Ce -β(Er-μNr) r

(62)

where

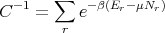C -1 = ∑ e- β(Er- μNr) r

(63)

It then follows that

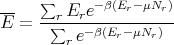∑ -β(E -μN ) -- --r Ere----r---r- E = ∑r e- β(Er- μNr)

(64)

and

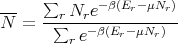∑ --- --r Nre--β(Er-μNr) N = ∑ e-β(Er- μNr) r

(65)

Let

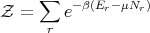Z = ∑ e- β(Er- μNr) r

(66)

Then

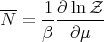N--= 1∂-lnZ- β ∂μ

(67)

Also

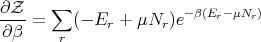∑ ∂Z--= (- Er + μNr )e-β(Er- μNr) ∂β r

(68)

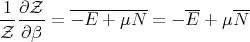-1 ∂Z-- ---------- -- --- Z ∂β = - E + μN = - E + μ N

(69)

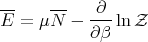-- --- ∂-- E = μ N - ∂β lnZ

(70)

The function 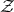is called the grand partition function. It is this function which is of primary importance in the grand canonical ensemble. We will return to a consideration of the grand canonical partition function when we begin our study of quantum statistical mechanics.

Before we begin a discussion of the applications of these basic concepts, two useful remarks need to be made. The first is the definition of the partition function within classical mechanics. In clasical mechanics, the sum over microstates is replaced by an integral over phase space. That is

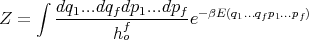∫ dq1...dqfdp1...dpf-- βE(q1...qfp1...pf) Z = hfo e

(71)

A second remark concerns the partition function of two independent systems. Let A and B be two independent systems both in contact with the same reservoir A^′. Let us label the microstates of system A by r and the microstates of system B by s. We will assume that the total energy E_rs of system A in microstate r and system B in microstate s is

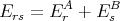Ers = EA + EB r s

(72)

The partition function of the combined system A plus B is

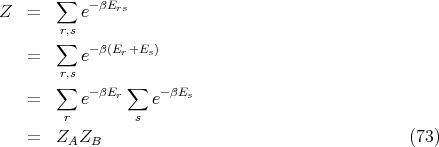
∑ -βErs Z = e r∑,s = e-β(Er+Es) r,s ∑ -βEr ∑ -βEs = r e s e = ZAZB (73)

Thus the partition function of two independent systems is just the product of the two independent partition functions. The only assumption has been that the energy of the total system can be expressed as the sum of the energies of the two individual independent systems. Notice that this means we can add free energies:

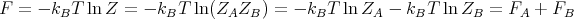F = - kBT lnZ = - kBT ln(ZAZB ) = - kBT lnZA - kBT ln ZB = FA + FB

(74)

The generalization to more than two systems is obvious. Assume we have N identical but independent systems. If ξ is the partition function of one system, then the total partition function of N systems is

Z = ξN

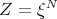(75)

We will find that quantum mechanics will lead to a correction to this equation under certain conditions.