LECTURE 11

Classical Ideal Monatomic Gas

The ideal gas is composed of noninteracting atoms. A monatomic gas can be considered to consist of mass points which have linear kinetic energy but no rotational kinetic energy, no vibrational energy and no internal excitations. Thus the total energy of an N particle ideal monatomic gas is

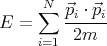
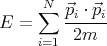∑N ⃗p ⋅ ⃗p E = -i---i i=1 2m

(1)

The classical partition function is

1 ∫ { [ 1 ( ) ]} Z ′ =--3N- exp - β ---- ⃗p21 + ⃗p22+ ...+ ⃗p2N d ⃗p1...d ⃗pNd⃗q1...d⃗qN h o 2m

(2)

The reason for the prime is that this partition function is slightly defective as we shall see. The integrals over the 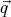_i’s gives a factor of V ^N. The integrals over momenta factorize into N separate integrals. So we can write:

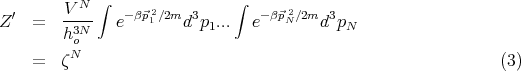
′ VN ∫ -β⃗p2∕2m 3 ∫ -β⃗p 2∕2m 3 Z = h3N- e 1 d p1... e N d pN No = ζ (3)

where

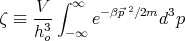V ∫ ∞ 2 ζ ≡ -3- e-β⃗p ∕2md3p ho -∞

(4)

is the partition function for a single molecule. So

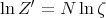′ ln Z = N ln ζ

(5)

It is straightforward to evaluate ζ:

∫ -V- ∞ -(β∕2m )⃗p2 3 ζ = h3 -∞ e d p o∫ ∫ ∞ ∫ = -V- e-(β∕2m)(p2x+p2y+p2z)dpxdpydpz h3o -∞ V [∫ ∞ 2 ]3 = --3 e-βp∕2mdp (6) h o -∞

Recall Reif Appendix A4:

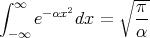∫ ∘ -- ∞ -αx2 π- -∞ e dx = α

(7)

So we evaluate the integral:

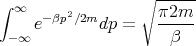∘----- ∫ ∞ - βp2∕2m π2m e dp = -β--- -∞

(8)

Hence

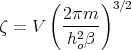( 2πm )3 ∕2 ζ = V ----- h2oβ

(9)

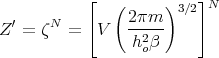⌊ ( )3∕2⌋N ′ N ⌈ 2πm-- ⌉ Z = ζ = V h2β o

(10)

and

[ ( ) ] ′ 3 3 2πm ln Z = N ln V - --lnβ + --ln --2-- 2 2 ho

(11)

From our previous equations we can calculate the mean pressure p, the mean energy E, and the specific heat C_V.

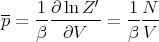′ p-= 1-∂-ln-Z--= 1-N-- β ∂V β V

(12)

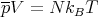-- pV = N kBT

(13)

This is the equation of state of the ideal gas. The mean energy is given by

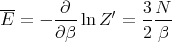-- -∂- ′ 3N-- E = - ∂β lnZ = 2 β

(14)

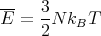E-= 3N k T 2 B

(15)

This is what we expect from the equipartition theorem. The heat capacity is given by

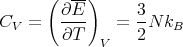( --) ∂E-- 3- CV = ∂T = 2N kB V

(16)

Using N = νN_a, where N_a is Avogadro’s number and ν is the number of moles, and R = N_ak_B, we get for the molar specific heat

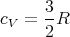3- cV = 2 R

(17)

This agrees with our previous result.

We can also calculate the entropy S:

[ ( ) ] ′ -- 3 3 2πm 3 S = kB [ln Z + βE ] = N kB ln V - -lnβ + --ln --2-- + -- 2 2 ho 2

(18)

[ 3 ] S = N kB lnV + 2-ln T + σ

(19)

where

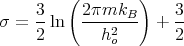( ) 3 2πmkB 3 σ = 2-ln --h2--- + 2- o

(20)

is a constant independent of T, V , and N. This expression for the entropy is wrong!

Gibbs Paradox

To see why (19) is wrong, note that as T → 0, S →-∞ instead of S → 0. This violates the third law of thermodynamics. But this is not surprising since classical statistical mechanics breaks down as T → 0. At low temperatures one must use quantum mechanics. Recall that S = k_B ln Ω where Ω is the number of accessible microstates. As T → 0, the only accessible microstate is the ground state. In addition the spacing of the microstates becomes larger than the temperature (ΔE > k_BT), and we must use quantum mechanics to address the discrete energy levels. So it’s not surprising that S doesn’t work at low temperatures.

But there’s another problem with S. Namely the entropy S does not scale with the size of the system as an extensive parameter should. In other words if V and N double, then the S and E should double. Consider a box with an internal partition. The total entropy is S₁ + S₂. We know this to be true since Z = Z₁Z₂ if systems 1 and 2 are completely independent, as they are in this example. Thus

-- S1 = kB [ln Z1 + βE1 ] -- S2 = kB [ln Z2 + βE2 ] (21)

and

S = k [lnZ Z + β(E- + E- )] B 1 2 -- 1 2 -- = kB[lnZ1 + β E1] + kB[lnZ2 + β E2 ] = S1 + S2 (22)

Now remove the partition. If the gases on the two sides are identical (N₁ = N₂, V ₁ = V ₂, and E₁ = E₂ and S₁ = S₂), then we will observe no physical changes. Nothing happens. Thus we would expect

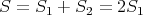S = S1 + S2 = 2S1

(23)

if the two sides are identical.

Now go back to our expression for the entropy of an ideal gas and note that

[ ] [ ] S (2N, 2V ) - 2S (N, V ) = 2N k ln(2V ) + 3ln T + σ - 2N k lnV + 3-lnT + σ B 2 B 2 = 2N kB ln2 ⁄= 0 (24)

The fact that S(2N, 2V ) - 2S(N,V )≠0 means something is wrong because the entropy is not additive. This problem is known as the “Gibbs paradox.”

If the gases on the two sides were different, then an increase in S when the partition function is removed seems reasonable since the two gases will diffuse and intermingle. In other words we expect the configurational entropy to increase. Then putting back the partition clearly would not restore the total system to its original state. On the other hand, if the gases are identical, then the restoration of the partition returns the system to a state physically indistinguishable from the initial state.

So if the gases on the two sides are identical, this increase in S does not make physical sense. The difficulty is associated with the concept of indistinguishability of the particles. If we exchange the positions of two identical particles, then we really haven’t changed any physical properties of the system. Yet we have counted these two identical microstates as truly distinct in calculating the entropy. (Recall S = k_B ln Ω.)

This concept of indistinguishability is clearly well established in quantum mechanics where this concept is basic to the theory. We have taken the classical picture of atoms too seriously and have finally exceeded the limits of classical validity.

Gibbs postulated that the classical partition function should be divided by N! to correct for counting each indistinguishable microstate. Let

′ Z = Z-- N !

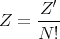(25)

Then

lnZ = lnZ ′ - N ln N + N

(26)

where Stirling’s approximation has been used. The entropy becomes

-- S = kB [ln Z + βE ] 3 = kBN [ln V + 2-lnT + σ] + kB [N - N ln N ] = kBN [ln V--+ 3-ln T + σ + 1 ] (27) N 2

V-- 3- S = kBN [ln N + 2 ln T + σo ]

(28)

where

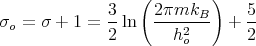( ) 3 2πmkB 5 σo = σ + 1 = 2-ln --h2--- + 2- o

(29)

Now when the system is doubled (N → 2N, V → 2V ), the entropy is doubled. Later when we repeat the calculation of the entropy of an ideal monatomic gas using quantum statistics, the factor of N! will arise naturally. Also the constant h_o will be identified as Planck’s constant.

It is interesting to note that this basic concept of quantum mechanics (indistinguishability of identical particles) did not arise spontaneously with the development of quantum mechanics, but was suggested by the ad hoc resolution of a paradox in classical statistical mechanics. Thus the Gibbs’ paradox joins black body radiation, the photoelectric effect, atomic line spectra and all the other pieces of evidence that led theorists to advance beyond classical mechanics to quantum mechanics.

Validity of the Classical Approximation

We have used a classical approximation to describe an ideal monatomic gas. Under what conditions would we expect it to be valid? One approach to answer this question begins with the uncertainty relation:

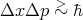Δx Δp ~> ¯h

(30)

We expect Δx <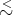
~ R where R is the mean separation of the ideal gas atoms, and Δp <
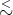~ p where p is the mean momentum. Then we would expect that classical mechanics would adequately describe the dynamics of the gas whenever

Rp--≫ ¯h

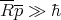(31)

This effectively says that ℏ is negligible. Recall that

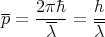p-= 2π¯h-= h- λ λ

(32)

where λ is the mean de Broglie wavelength. Then

-- Rp--≫ ¯h

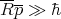(33)

becomes

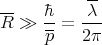-- -- ¯h λ R ≫ --= --- p 2π

(34)

Or more simply, the classical description applies when

-- -- R ≫ λ

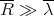(35)

i.e., the mean separation between particles is much greater than their mean de Broglie wavelength.

To estimate R, imagine each molecule at the center of a little cube of side R, these cubes filling the available volume V . Then

--3 R N = V

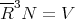(36)

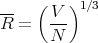( )1∕3 -- V-- R = N

(37)

The mean momentum p can be estimated using the equipartition theorem

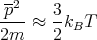-- p2-- 3- 2m ≈ 2kBT

(38)

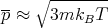∘ -------- p-≈ 3mkBT

(39)

and

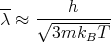λ-≈ √---h----- 3mkBT

(40)

Hence the condition that the classical description should be valid is

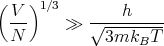( )1 ∕3 V-- √---h----- N ≫ 3mkBT

(41)

So for large masses and high temperatures we expect classical mechanics to hold.

As an example, air at standard temperature and pressure (STP) has T = 300 K and mean pressure P = 760 mm of Hg (mercury) = 1.01 × 10⁵ Newton/m². 80% of air is N₂. So the mass of a nitrogen molecule is m = 28m_p where m_p = 1.67 × 10^-27 kilograms is the mass of a proton. Using k_B = 1.38 × 10^-23 Joules/K, we obtain

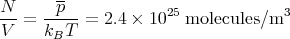-- N-- --p-- 25 3 V = kBT = 2.4 × 10 molecules∕m

(42)

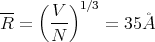( ) -- V--1∕3 R = N = 35˚A

(43)

and

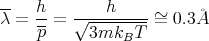-- h- ----h-----~ ˚ λ = p-= √3mk----T-= 0.3A B

(44)

Thus

-- -- R ≫ λ

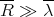(45)

So the classical description holds for air. However, this is not the case for an electron gas in a metal at 300 K. In that case we find R 2 or 3 Å and λ 60 Å (using the electron mass). Thus λ ≫R and we must use a full quantum treatment for an electron gas.

Classical Theory of the Specific Heat of Solids

Consider a monatomic solid as a collection of N independent, identical atoms of mass m, all of which vibrate harmonically about their equilibrium positions at frequency ω. The total energy of the solid is

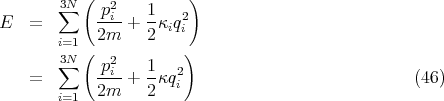
( ) ∑3N -p2i- 1- 2 E = 2m + 2κiqi i=1 ( ) ∑3N p2i 1 2 = 2m--+ 2κqi (46) i=1

if all the spring constants κ are equal. By the equipartition theorem

E- = (number of quadratic terms in E ) × 1k T 2 B = 3N kBT (47)

and the molar specific heat becomes simply

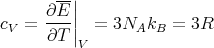--| ∂-E-|| cV = ∂T || = 3NAkB = 3R V

(48)

where N_A is Avogadro’s number (N_A = 6.02 × 10²³ molecules/mole) or

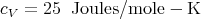cV = 25 Joules∕mole - K

(49)

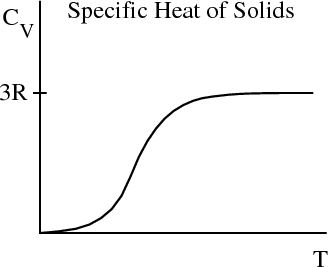
Notice that the specific heat is a constant independent of T. This is is called the Dulong–Petit value of the specific heat. The values of c_p for some common substances at room temperature in units of Joules mole^-1 K^-1 are (from Reif p. 254):

solid

c_p

solid

c_p

24.5

24.4

25.5

26.4

22.4

25.4

C (diamond)

6.1

Note the obvious discrepancy with carbon (diamond). The classical theory predicts a temperature independent specific heat while all materials have the general property that c_V is relatively temperature independent at high temperature but goes to zero as T → 0 as required by the third law of thermodynamics. Page 256 of Reif displays actual data for the specific heat of diamond. From the graph one can see that above about 1000 K, diamond has a specific heat of approximately 25 Joules/mole–K.

spHt.eps

Einstein Model of Specific Heat

To get the proper temperature dependence of the specific heat of solids, we must use quantum mechanics to take into account the discrete energy levels that become apparent at low energies and low temperatures. One of the simplest ways to do this is provided by the Einstein model of specific heat. As a simple model Einstein proposed a collection of N independent, identical harmonic oscillators but treated the oscillators in quantum mechanical rather than classical terms. Let the spring constant κ_i = mω_i² = mω² = constant for all atoms in the monatomic solid. Then

3∑N ( 2 ) E = -pi-+ 1m ωq2i i=1 2m 2

(50)

The partition function for N identical independent harmonic oscillators is

3N Z = ζ

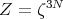(51)

where

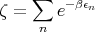∑ ζ = e-βϵn n

(52)

The energy levels of a single one dimensional harmonic oscillator are

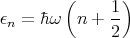( 1 ) ϵn = ¯hω n + -- 2

(53)

where n = 0, 1, 2,.... Then

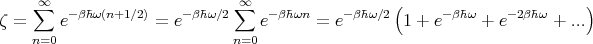∞∑ - β¯hω(n+1∕2) -β¯hω∕2∑∞ - β¯hωn -β¯hω∕2( -β¯hω - 2β¯hω ) ζ = e = e e = e 1 + e + e + ... n=0 n=0

(54)

The sum is just an infinite geometric series where each term is obtained from the preceding one as a result of multiplication by e^-βℏω. We can easily sum the series to get

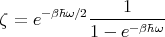ζ = e-β¯hω∕2----1----- 1 - e-β¯hω

(55)

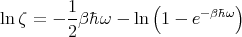ln ζ = - 1-β¯hω - ln (1 - e-β¯hω) 2

(56)

and

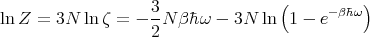( ) ln Z = 3N ln ζ = - 3N β¯h ω - 3N ln 1 - e-β¯hω 2

(57)

We can now obtain the mean energy:

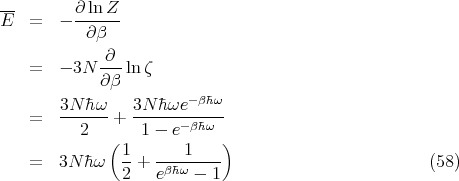
-- ∂ ln Z E = - ------ ∂β ∂-- = - 3N ∂β lnζ -β¯hω = 3N-¯hω-+ 3N-¯hωe------ 2 1 - e-β¯hω ( 1 1 ) = 3N ¯hω -+ -β¯hω----- (58) 2 e - 1

and the heat capacity:

--| ∂ E || CV = ∂T--|| --V| ∂-E-|| ∂-β = ∂ β || ∂T V ( --) --1--- ∂-E- = - kBT 2 ∂ β [ Vβ¯hω ] = - 3N-¯hω- - --e---¯h-ω-- kBT 2 (eβ¯hω - 1)2 ( )2 β¯hω ¯h-ω-- ---e------- = 3N kB kBT (eβ¯hω - 1 )2 (59)

It is customary to define a quantity called the Einstein temperature θ_E by

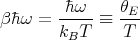β¯h ω = -¯hω--≡ θE- kBT T

(60)

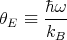¯h-ω θE ≡ k B

(61)

Then the molar specific heat becomes (with N = N_A)

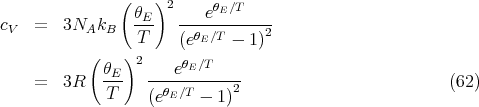
( ) θE 2 e θE∕T cV = 3NAkB T-- --θE∕T-----2 ( ) (e - 1) θE 2 eθE ∕T = 3R --- --θE∕T-----2 (62) T (e - 1)

In the high temperature limit of T →∞ or θ_E∕T → 0, we can expand the exponential in the denominator:

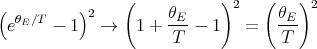( )2 ( )2 ( )2 eθE∕T - 1 → 1 + θE- - 1 = θE- T T

(63)

and

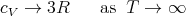c → 3R as T → ∞ V

(64)

In the low temperature limit where T → 0 or θ_E∕T →∞

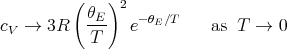( )2 θE- -θE∕T cV → 3R T e as T → 0

(65)

Careful experiments indicate that c_V goes as T³ at low temperatures rather than exponentially. The explanation will come later when we consider the Debye theory of collective oscillations or normal modes of a crystalline solid consisting of a lattice of atoms.