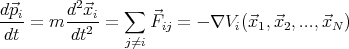
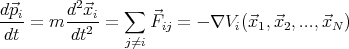 | (1) |
where 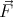 ij is the force on the ith particle produced by the jth particle. V i is the total potential
energy of the ith particle assuming that all the forces are conservative. We must also specify
the initial conditions, i.e., the initial positions and velocities of all the particles. Then we must
solve the N coupled second order partial differential equations. This is quite a daunting task.
It’s true that we now have powerful computers and molecular dynamics simulations carry out
such tasks, but they can only handle a few thousand particles and track their motions for
perhaps a few times 10-8 seconds. So we throw up our hands. This is not the way to
go.
ij is the force on the ith particle produced by the jth particle. V i is the total potential
energy of the ith particle assuming that all the forces are conservative. We must also specify
the initial conditions, i.e., the initial positions and velocities of all the particles. Then we must
solve the N coupled second order partial differential equations. This is quite a daunting task.
It’s true that we now have powerful computers and molecular dynamics simulations carry out
such tasks, but they can only handle a few thousand particles and track their motions for
perhaps a few times 10-8 seconds. So we throw up our hands. This is not the way to
go.
Fortunately, there is a better way. We can use the fact that there are large numbers of particles to apply a statistical analysis to the situation. We are usually not interested in the detailed microscopics of a liquid or a gas. Instead we are usually interested in certain macroscopic quantities like
These concepts don’t make sense for one atom or even a few particles. For example, what is the temperature of one atom? That doesn’t make sense. But if we have a whole bucket of atoms, then temperature makes sense. Since we are not concerned with the detailed behavior of each and every particle, we can use statistical methods to extract information about a system with N ≫ 1 interacting particles. For example, we may be interested in the average energy of the system, rather than the energy of each particle. Statistical methods work best when there are large numbers of particles. (Think of polling.) Typically we have on the order of a mole’s worth of particles. A mole is the number of atoms contained in 12 grams of carbon 12. (A carbon 12 atom has 6 protons and 6 neutrons for a total 12 nucleons. Its atomic weight is 12.) So a mole has 6.022 × 1023 atoms. This is called Avogadro’s number.
There are two basic approaches to describing the properties of a large number of particles:
 | (2) |
Now suppose we want the number of configurations with n up sites, regardless of what order they’re in. The number of down sites will be N-n, since the total number of sites is N. The number of such configurations is
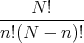 | (3) |
To see where this comes from, suppose we have N spins of which n are up and (N-n) are down. How many ways are there to arrange them? Recall that the number of ways to arrange N objects with one object on each site (or in each box) is
etc. until the last place can be occupied by the last 1 object. So there are
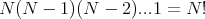 | (4) |
configurations. In these configurations the n up spins can be arranged in any of n! ways. Also the remaining (N-n) sites have down spins which can be arranged in any of (N -n)! ways. The spins are regarded as distinguishable. So there are 2 ways to have ↑↑: ↑↑ and ↑↑. They look the same, but if one were red and the other blue, you would see the difference (red, blue) and (blue, red). We are dividing out this overcounting; that’s what the denominator n!(N - n)! is for.
So the probability of a state with n up spins and (N-n) down spins is
Now suppose that the probability of a site getting ↑ is p and the probability of getting ↓ is q = 1 -p. So far we have considered up and down to be equally probable, so p = q = 1∕2. But what if p≠q? This might be caused by an external magnetic field which biases the spins one way or another. If we have 2 spins, the probability of getting 2 up spins is p2. (Recall that the probability of flipping a coin twice and getting heads both times is 1/4.) If we want n up spins and (N-n) down spins, then the probability is
When p = q = 1∕2, this reduces to our previous result (5). Equation (6) is called the binomial distribution because the prefactor N!∕n!(N - n)! is the coefficient in the binomial expansion:
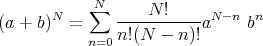 | (7) |
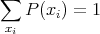 | (8) |
In other words, the probability distribution function P(xi) is normalized to one. One can also have a probability distribution function P(x) of a continuous variable x. For example, suppose you leave a meter stick outside on the ground. P(x)dx could be the probability that the first raindrop to hit the stick will strike between position x and x + dx. P(x) is called the probability density. The normalization condition is
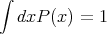 | (9) |
Note that ∫ dxP(x) is the area under the curve P(x). The normalization sets this area equal to 1.
The average of some quantity x is
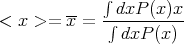 | (10) |
Averages can be denoted by < x > or x. For a discrete quantity
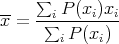 | (11) |
If the probability is normalized, then the denominator is 1. For example, suppose N(Ai) is the number of people with age Ai. Then the average age is
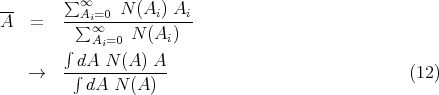
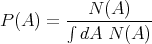 | (13) |
Notice that this satisfies the normalization condition. More generally, if f(x) is a function of x, then the average value of f(x) is
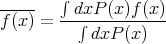 | (14) |
One of the more useful functions concerns the deviation of x from the mean x:
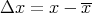 | (15) |
Then

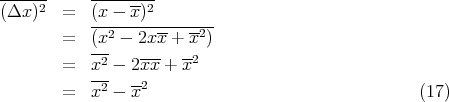
In general the nth moment of x about its mean is given by
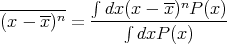 | (18) |
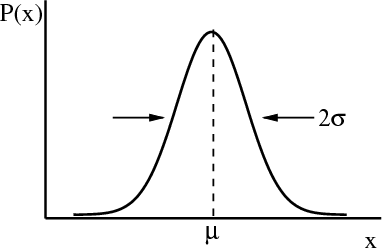
Two other terms that are often used are the most probable value of x and the median. The most probable value of x is the maximum of P(x). The median xmed is the value of x such that half the values of x are greater than xmed, i.e., x > xmed, and half the values of x are less than xmed, i.e., x < xmed. In terms of the area under the curve, the median is the vertical dividing line such that half the area lies to the left of the median and half to the right of the median.
The formula for a Gaussian distribution is
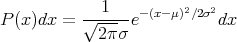 | (19) |
where μ = x is the mean. The coefficient is set so that the normalization condition is satisfied. σ2 = (Δx)2 = (x -x)2. 2σ is the width of the distribution. There is a 68% chance that -σ ≤ x ≤ σ. One obtains this by integrating P(x) from -σ to +σ. σ is sometimes called the root–mean–square (rms) deviation or the standard deviation. You will have the opportunity to check some of these assertions in your homework.
For a Gaussian distribution, all the higher moments can be expressed in terms of the first and second moments. For example (x -x)4 = 3(x -x)2.
There is one other interesting aspect of Gaussian distributions. It’s called the central limit theorem. It can be stated in terms of a random walk in one dimension. A drunk starts at a lamp post and staggers back and forth along the one dimensional sidewalk. Let w(s)ds be the probability that a step length lies in the range between s and s + ds. No matter what the probability distribution w(s) for each step may be, as long as the steps are statistically independent and w(s) falls off rapidly enough as |s|→∞, the total displacement x will be distributed according to the Gaussian law if the number of steps N is sufficiently large. This is called the central limit theorem. It is probably the most famous theorem in mathematical probability theory. The generality of the result also accounts for the fact that so many phenomena in nature (e.g., errors in measurement) obey approximately a Gaussian distribution.
In fact, if we go back to the binomial distribution given in eq. (6), then in the limit of large N, this becomes the Gaussian distribution (see Reif 1.5). In this case, x represents the net magnetization, i.e., the difference between the number of up and down spins:
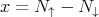 | (20) |
The average magnetization
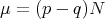 | (21) |
and the mean square deviation is
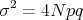 | (22) |
(Reference: Howard C. Berg, Random Walks in Biology.)
The random walk is an important concept. Let us go back to the drunk starting at the lamp post and stumbling either to the right or the left. Consider an ensemble of M drunks. Let xi(N) be the position of the ith drunk after N steps. Suppose everyone starts at the origin so that xi(N = 0) = 0 for all i. Let the step size be of fixed length s. Then
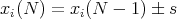 | (23) |
The average displacement from the origin is
![-- 1 ∑M
x(N ) = M-- xi(N )
i=1
1 ∑M
= M-- [xi(N ) = xi(N - 1 ) ± s]
i=1
1 ∑M
= --- xi(N - 1)
M- i=1
= x(N - 1)
= 0 (24)](lecture125x.png)
It is useful to look at the spread in positions. A convenient measure of spreading is the
root-mean-square (rms) displacement 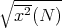 . Here we average the square of the displacement
rather than the displacement itself. Since the square of a negative or a positive number is
positive, the result will be positive.
. Here we average the square of the displacement
rather than the displacement itself. Since the square of a negative or a positive number is
positive, the result will be positive.
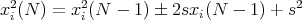 | (25) |
Then we compute the mean,
![--2 1 ∑M 2
x i(N ) = M-- xi(N )
i=1
1 ∑M [ 2 2]
= M-- xi(N - 1) ± 2sxi(N - 1) + s
---i=1
= x2i(N - 1) + s2 (26)](lecture128x.png)
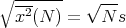 | (27) |
The rms displacement is a good measure of the typical distance that the drunk reaches. Notice that it goes as the square root of the number of steps. If τ is the time between successive steps, then it takes a time t = Nτ to take N steps. So
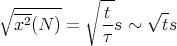 | (28) |
Notice that the rms displacement goes as square root of the time t.
A random walk is what particles execute when they diffuse. Think of a opening a bottle of perfume. The perfume molecules diffuse through the air. We can define a diffusion coefficient D by
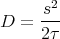 | (29) |
(The factor of 2 is by convention.) Then in one dimension

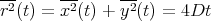 | (31) |
Similarly for 3 dimensions
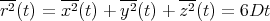 | (32) |
Notice that in all dimensions, the mean square displacement is linear in the number of steps N and in the time t. The diffusion coefficient D characterizes the migration of particles in a given kind of medium at a given temperature. In general, it depends on the size of the particle, the structure of the medium, and the absolute temperature. For a small molecule in water at room temperature, D ≃ 10-5 cm2/sec.
If we go back to the drunk who is taking steps of size s to the right or to the left, then we can use the binomial distribution. Let p be the probability to take a step to the right and q = 1 -p be the probability to take a step to the left. After taking N steps, the mean number n1 of steps to the right is (see Reif Eq. (1.4.4)):
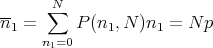 | (33) |
The mean number of steps to the left is
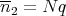 | (34) |
Let the displacement be
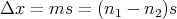 | (35) |
The mean displacement is (Reif Eq. (1.4.6)):
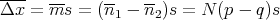 | (36) |
So if p = q = 1∕2, then the mean displacement Δx = 0.
The displacement squared is
 | (37) |
The dispersion of the net displacement or the mean square displacement is
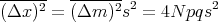 | (38) |
where we used Reif Eq. (1.4.12). If p = q = 1∕2, then the mean square displacement (Δx)2 = Ns2 which is what we got before. The rms displacement is
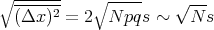 | (39) |
If p = q = 1∕2, then the rms displacement is 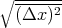 =
= 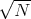 s which is what we got before.
Notice again that the rms displacement goes as the square root of the number of steps. Again
the characteristic or typical displacement is given by
s which is what we got before.
Notice again that the rms displacement goes as the square root of the number of steps. Again
the characteristic or typical displacement is given by 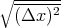 ~
~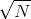 s.
s.
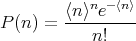 | (40) |
where the mean number of desired events is ⟨n⟩ = Np. You will derive the Poisson distribution in your homework starting from the binomial distribution.
Example: Let us consider the problem mentioned above. If on average there is one bad penny in 1000, what is the probability that no bad pennies will be found in a given sample of 100 pennies?
Solution: We are interested in the outcome that there is a bad penny. The probability of getting a bad penny is p = 1∕1000 = 0.001. The number of trials is N = 100. So the average number ⟨n⟩ of bad pennies in 100 is ⟨n⟩ = Np = 100∕1000 = 0.1. The probability of finding no bad pennies is P(n = 0) which is given by
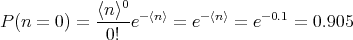 | (41) |
Alternative solution: The probability of getting a bad penny is p = 1∕1000 = 0.001. The probability of not getting a bad penny is q = 1 - p = 0.999. So the probability of no bad pennies in 100 is P(n = 0) = qN = (0.999)100 = 0.905 which agrees with our previous result.
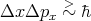 | (42) |
So the wavefunction of a particle is written ψ(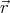 ). The wavefunction is determined by
Schroedinger’s equation
). The wavefunction is determined by
Schroedinger’s equation
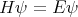 | (43) |
where H is the Hamiltonian and E is the energy. The Hamiltonian is the sum of the kinetic and potential energies. You solve Schroedinger’s equation to determine the wavefunction. Schroedinger’s equation can be written as a matrix equation or as a second order differential equation. Often the wavefunction solutions are labeled by definite values of energy, momentum, etc. These values can only have discrete values, i.e., they are quantized. They are called quantum numbers. We can label the different wavefunction solutions by their quantum numbers. Quantum numbers correspond to conserved quantities like energy, momentum, angular momentum, spin angular momentum, etc. Perhaps the most familiar example of this is the electronic orbitals in the hydrogen atom. The electron orbitals, like the 1s and 2p states, have definite discrete energies and definite values of the orbital angular momentum. For example, the energy of the 1s state in hydrogen is 1 Rydberg or 13.6 eV. The electron in this state can be described by a wavefunction ψ1s(r). The quantum numbers of this state are n = 1 and L = 0. n = 1 means that it has energy E1 = 13.6 eV and L is the orbital angular momentum. (s is the spectroscopic notation for L = 0.) Solving the Schroedinger equation for the hydrogen atom yields many wavefunctions or orbitals (1s, 2s, 2px, 2py, 2pz, 3s, etc.).
Another example is a particle in a box.
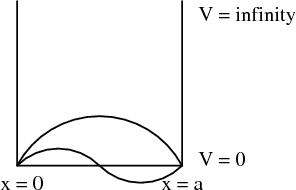
The energy eigenvalues
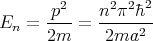 | (44) |
Each value of n corresponds to a different eigenvalue of the energy En. Notice that the energy levels are not equally spaced; they get farther apart as you go up in energy. Each value of n also corresponds to a different wavefunction
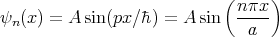 | (45) |
Notice that the more nodes there are, the more wiggles there are, and the higher the energy is.
A harmonic oscillator is another example. This is just the quantum mechanical case of a mass attached to a spring. In this case the potential is a parabola rather than being a square well. A particle of mass m in this potential oscillates with frequency ω. The Hamiltonian is
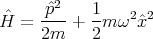 | (46) |
You will learn how to solve this in your quantum mechanics course. Let me just write down the result. The energy eigenvalues are
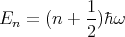 | (47) |
where n = 0, 1, 2, 3,.... Notice once again that the energy levels are quantized. In this case they are evenly spaced by an amount ΔE = ℏω. The harmonic oscillator has Gaussian wavefunctions (Hermite polynomials).
Wavefunctions can describe more than one particle. You can have a wavefunction associated
with a state with many particles. We call this a many body wavefunction. In this case we can
describe a state with N particles by ψ{n}(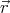 1,
1,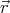 2,...,
2,...,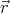 N). The subscript {n} denotes the quantum
numbers that label the wavefunction.
N). The subscript {n} denotes the quantum
numbers that label the wavefunction.